题目内容
9. 在△ABC中,∠C=∠ABC,AE∥BC,BE平分∠ABC,则下列结论中一定成立的是①②④(把所有正确结论的序号都填在横线上).
在△ABC中,∠C=∠ABC,AE∥BC,BE平分∠ABC,则下列结论中一定成立的是①②④(把所有正确结论的序号都填在横线上).①AE平分∠DAC ②∠C=2∠E
③在△ABE中,AC平分∠BAE
④若AC⊥BE,则∠E=30°.
分析 求出∠CBA=2∠CBE=2∠EBA,∠CBE=∠EBA,根据平行线的性质求出∠CAE=∠C,∠EAD=∠CAB,求出AC=AB,∠CAE=∠EAD,根据平行线的性质得出∠E=∠CBE,求出∠C=∠CBA,∠CBA=2∠CBE,推出∠C=2∠E,∠E=∠EBA,但是不能推出AC平分∠EAB,证△CFB≌△AFB,推出BC=AB,得出△ABC是等边三角形,求出∠CBA=60°,根据以上结论逐个判断即可.
解答 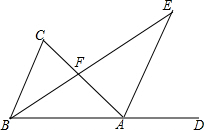 解:如图,∵BE平分∠CBA,
解:如图,∵BE平分∠CBA,
∴∠CBA=2∠CBE=2∠EBA,∠CBE=∠EBA,
∵AE∥BC,
∴∠CAE=∠C,∠EAD=∠CAB,
∵∠C=∠ABC,
∴AC=AB,∠CAE=∠EAD,
∴AE平分∠CAD,∴①正确;
∵AE∥BC,
∴∠E=∠CBE,
∵∠C=∠CBA,∠CBA=2∠CBE,
∴∠C=2∠E,∴②正确;
能推出∠E=∠EBA,但是不能推出AC平分∠EAB,∴③错误;
∵AC⊥BE,
∴∠CFB=∠AFB=90°,
在△CFB和△AFB中
$\left\{\begin{array}{l}{∠CFB=∠AFB}\\{BF=BF}\\{∠CBF=∠ABF}\end{array}\right.$
∴△CFB≌△AFB(ASA),
∴BC=AB,
∵AC=AB,
∴BC=AC=AB,
∴△ABC是等边三角形,
∴∠CBA=60°,
∵BE平分∠CBA
∵∠E=∠CBE=∠EBA=30°,∴④正确.
故答案为:①②④.
点评 本题考查了等腰三角形的性质和判定,全等三角形的性质和判定,等边三角形的性质和判定的应用,能综合运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
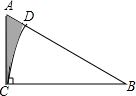 如图,△ABC中,∠ACB=90°,AB=2AC=6,以B为圆心BC为半径作弧交AB于点D,则阴影部分的面积为$\frac{9\sqrt{3}}{2}$-$\frac{9π}{4}$.
如图,△ABC中,∠ACB=90°,AB=2AC=6,以B为圆心BC为半径作弧交AB于点D,则阴影部分的面积为$\frac{9\sqrt{3}}{2}$-$\frac{9π}{4}$.