题目内容
19．求$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$的值．分析 设$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$=m，从而得出m2=2-$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$=2-m，解关于m的方程即可，m是非负数，再取舍即可．
解答 解：设$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$=m，
∴m2=2-$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$，
∴m2=2-m，
∴m2+m-2=0，
∴m1=-2（舍），m2=1，
∵m是非负数，
∴m=1，
∴$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$的值为1．
点评 本题考查了二次根式的化简求值，设出$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$=m是解题的关键．
练习册系列答案
53天天练系列答案
相关题目
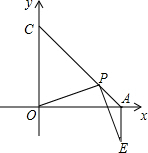已知∠AC0=45°，P是线段AC上任一点，（P不与A、C重合），连OP，作PE⊥OP，且PE=OP，连AE，试判断AE和OA的位置关系，请说明理由．
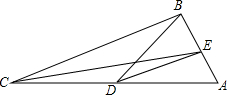如图，在△ABC中，∠ABC=100°，CE平分∠ACB交AB于点E，点D在AC上，且∠CBD=20°．