题目内容
14.在矩形ABCD中,AB=3,AD=4,点P是对角线AC上的一动点(点P与点A、C不重合)(1)如图1,如果AP=3,求△PAB的面积;
(2)如图2,过点P作PQ⊥PB,PQ分别交射线BC和射线DC于点E、Q.
①设PB=x,PQ=y,求y关于x的函数关系式,并写出函数定义域;
②如果CQ=1,写出AP的长.(不必写出解题过程)

分析 (1)作PG⊥AB于G,根据平行线的性质得到$\frac{AP}{AC}$=$\frac{GP}{BC}$,代入计算求出PG,根据三角形的面积公式计算即可;
(2)①过P作MN∥BC交AB于M,交DC于N,证明△PMB∽△QNP,得到$\frac{PB}{PQ}$=$\frac{BM}{PN}$=$\frac{3}{4}$,代入即可得到y关于x的函数关系式;
②设CN=3a,则PN=4a,PC=5a,NQ=3a+1,根据△PMB∽△QNP得到比例式,求出a的值,计算即可.
解答  解:如图1,作PG⊥AB于G,
解:如图1,作PG⊥AB于G,
∵∠ABC=90°,AB=3,AD=4,
∴AC=5,
∵PG⊥AB,∠ABC=90°,
∴PG∥BC,
∴$\frac{AP}{AC}$=$\frac{GP}{BC}$,
∴GP=$\frac{12}{5}$,
∴△PAB的面积=$\frac{1}{2}$×3×$\frac{12}{5}$=$\frac{18}{5}$;
(2)①如图2,过P作MN∥BC交AB于M,交DC于N,
则BM=CN,
∵PN∥AD,
∴$\frac{CN}{PN}$=$\frac{CD}{AD}$=$\frac{3}{4}$,
∴$\frac{BM}{PN}$=$\frac{3}{4}$,
∵∠MPB+∠QPN=90°,∠Q+∠QPN=90°,
∴∠MPB=∠Q,又∠PMB=∠QNP=90°,
∴△PMB∽△QNP,
∴$\frac{PB}{PQ}$=$\frac{BM}{PN}$=$\frac{3}{4}$,即y=$\frac{4}{3}$x($\frac{12}{5}$≤x≤4);
②设CN=3a,则PN=4a,PC=5a,NQ=3a+1,
∵△PMB∽△QNP,
∴$\frac{NQ}{MP}$=$\frac{PN}{MB}$,即$\frac{3a+1}{4-4a}$=$\frac{4a}{3a}$,
解得,a=$\frac{13}{25}$,
则PC=5a=$\frac{13}{5}$,
∴AP=5-$\frac{13}{5}$=$\frac{12}{5}$.
点评 本题考查的是矩形的性质、相似三角形的判定和性质,正确作出辅助线、灵活运用相关的定理是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | m≠3 | B. | m≠0或m≠3 | C. | m≠0 | D. | m≠0且m≠3 |
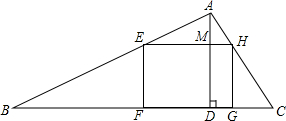 如图,矩形EFGH内接于△ABC,AD⊥BC于点D,交EH于点M,BC=48cm,AD=16cm,EF:FG=5:9.求矩形EFGH的面积.
如图,矩形EFGH内接于△ABC,AD⊥BC于点D,交EH于点M,BC=48cm,AD=16cm,EF:FG=5:9.求矩形EFGH的面积. 如图:
如图: 如图,点0是线段CD的中点,以点0为旋转中心,画出与已知图形成中心对称的图形.
如图,点0是线段CD的中点,以点0为旋转中心,画出与已知图形成中心对称的图形.