题目内容
10.已知:$\sqrt{a+4}$+b2-6b+9=0,求(a+b)2的值.分析 将代数式中的b2-6b+9配方后利用非负数的性质确定a、b的值,从而确定代数式的值即可.
解答 解:原式可变形为$\sqrt{a+4}$+(b-3)2=0,
∵$\sqrt{a+4}$≥0,(b-3)2≥0,
∴a+4=0,b-3=0,
∴a=-4,b=3,
∴a+b=-4+3=-1,
∴(a+b)2=(-1)2=1.
点评 本题考查了配方法的应用、非负数的性质、算术平方根的知识,属于基础知识,解题的关键是对代数式进行正确的配方.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
20.已知等腰三角形的两边长分别为4和6,则底边上的高的平方等于( )
| A. | 7 | B. | 7或41 | C. | 32 | D. | 32或7 |
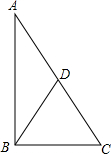 如图,已知Rt△ABC中,∠ABC=90°,△ABC的周长为17cm,斜边上中线BD长为$\frac{7}{2}$cm.则该三角形的面积为$\frac{51}{4}$cm2.
如图,已知Rt△ABC中,∠ABC=90°,△ABC的周长为17cm,斜边上中线BD长为$\frac{7}{2}$cm.则该三角形的面积为$\frac{51}{4}$cm2.