题目内容
9.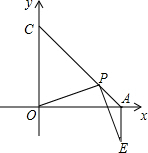 已知∠AC0=45°,P是线段AC上任一点,(P不与A、C重合),连OP,作PE⊥OP,且PE=OP,连AE,试判断AE和OA的位置关系,请说明理由.
已知∠AC0=45°,P是线段AC上任一点,(P不与A、C重合),连OP,作PE⊥OP,且PE=OP,连AE,试判断AE和OA的位置关系,请说明理由.
分析 作OG⊥AC,EF⊥AC,垂足分别为G、F,首先利用等腰直角三角AOC,得出条件证得△OGP≌△PFE,OG=PF=AG,GP=EF,进一步证得△AEF是等腰直角三角形得出结论AE⊥OA即可.
解答 AE⊥OA.
证明:如图,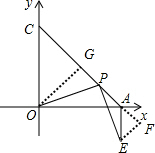
作OG⊥AC,EF⊥AC,垂足分别为G、F,
∵∠AC0=45°,∠A0C=90°,
∴∠OAC=∠OCA=45°,
∴OA=OC,
∴OG=CG=AG,
∵PE⊥OP,
∴∠OPG+∠EPF=∠GOP+∠OPG=90°,
∴∠GOP=∠EPF,
在△OGP和△PFE中,
$\left\{\begin{array}{l}{∠GOP=∠FPE}\\{∠OGP=∠EFP}\\{OP=PE}\end{array}\right.$,
∴△OGP≌△PFE,
∴OG=PF=AG,GP=EF,
∴AG-AP=PF-AP,
∴GP=AF=EF,
∴∠EAF=45°,
∴AOE=90°,
∴AE⊥OA.
点评 此题考查三角形全等的判定与性质,等腰直角三角形的性质,正确作出辅助线,构造出全等的三角形是解决问题的关键.

练习册系列答案
相关题目
4.函数y=$\frac{m(m-3)}{x}$是反比例函数,则m必须满足( )
| A. | m≠3 | B. | m≠0或m≠3 | C. | m≠0 | D. | m≠0且m≠3 |
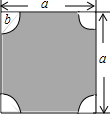 如图,四个角是半径为b的$\frac{1}{4}$的圆形.请用图中的字母表示阴影部分的面积.
如图,四个角是半径为b的$\frac{1}{4}$的圆形.请用图中的字母表示阴影部分的面积.
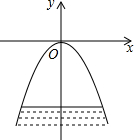 如图,拱桥的形状是抛物线,其函数关系式为y=$\frac{1}{3}$x2,当水面离桥顶的高度为$\frac{25}{3}$米时,水面的宽度为10米.
如图,拱桥的形状是抛物线,其函数关系式为y=$\frac{1}{3}$x2,当水面离桥顶的高度为$\frac{25}{3}$米时,水面的宽度为10米.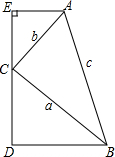 如图,在四边形ABDE中,∠E=90°,AE∥BD,C为ED上一点,设△ABC三边分别为a、b、c,且方程(a+c)x2-2bx-a+c=0有两相等实根.
如图,在四边形ABDE中,∠E=90°,AE∥BD,C为ED上一点,设△ABC三边分别为a、b、c,且方程(a+c)x2-2bx-a+c=0有两相等实根.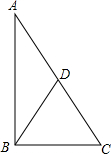 如图,已知Rt△ABC中,∠ABC=90°,△ABC的周长为17cm,斜边上中线BD长为$\frac{7}{2}$cm.则该三角形的面积为$\frac{51}{4}$cm2.
如图,已知Rt△ABC中,∠ABC=90°,△ABC的周长为17cm,斜边上中线BD长为$\frac{7}{2}$cm.则该三角形的面积为$\frac{51}{4}$cm2.