题目内容
4.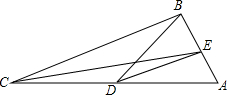 如图,在△ABC中,∠ABC=100°,CE平分∠ACB交AB于点E,点D在AC上,且∠CBD=20°.
如图,在△ABC中,∠ABC=100°,CE平分∠ACB交AB于点E,点D在AC上,且∠CBD=20°.(1)求证:BA是△CBD的外角平分线;
(2)求∠CED的度数.
分析 (1)根据题意和邻补角的性质分别求出∠DBA和∠PBA的度数,即可证明;
(2)作EF⊥AC于F,EG⊥BD于G,EH⊥CB于H,根据角平分线的性质证明DE平分∠BDA,得到答案.
解答 (1)证明:∵∠ABC=100°,∠CBD=20°
∴∠DBA=80°,
∴∠PBA=80°,
∴∠DBA=∠PBA,
∴BA是△CBD的外角平分线;
(2)解:作EF⊥AC于F,EG⊥BD于G,EH⊥CB于H,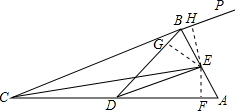 ∵CE平分∠ACB,EF⊥AC,EH⊥CB,
∵CE平分∠ACB,EF⊥AC,EH⊥CB,
∴EF=EH,
同理,EG=EH,
∴EF=EG,又EF⊥AC,EG⊥BD,
∴DE平分∠BDA,
∴∠CED=$\frac{1}{2}$∠CBD=10°.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
12.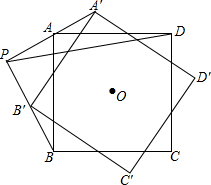 如图,点O是正方形ABCD中的对称中心,AB=2,将正方形ABCD绕点O旋转任意角度至正方形A′B′C′D′,直线AA′与直线BB′交于点P,则线段PD长度的最大值为( )
如图,点O是正方形ABCD中的对称中心,AB=2,将正方形ABCD绕点O旋转任意角度至正方形A′B′C′D′,直线AA′与直线BB′交于点P,则线段PD长度的最大值为( )
 如图,点O是正方形ABCD中的对称中心,AB=2,将正方形ABCD绕点O旋转任意角度至正方形A′B′C′D′,直线AA′与直线BB′交于点P,则线段PD长度的最大值为( )
如图,点O是正方形ABCD中的对称中心,AB=2,将正方形ABCD绕点O旋转任意角度至正方形A′B′C′D′,直线AA′与直线BB′交于点P,则线段PD长度的最大值为( )| A. | $\sqrt{5}$ | B. | 1 | C. | $\sqrt{5}$+1 | D. | $\sqrt{5}$-1 |
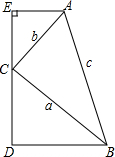 如图,在四边形ABDE中,∠E=90°,AE∥BD,C为ED上一点,设△ABC三边分别为a、b、c,且方程(a+c)x2-2bx-a+c=0有两相等实根.
如图,在四边形ABDE中,∠E=90°,AE∥BD,C为ED上一点,设△ABC三边分别为a、b、c,且方程(a+c)x2-2bx-a+c=0有两相等实根.