题目内容
7.用一个正方形框出9个数,要使这个正方形框出的9个数之和分别等于(1)1998(2)2011,这是否可能?若可能,求出框中最大数和最小数.若不可能,说明理由.| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 |
| … | … | … | … | … | … |
| 997 | 998 | 999 | 1000 | 1001 | 1002 |
| … | … | … | … | … | … |
分析 设最小的数为x,根据图形可以知道另外8个数分别为:x+1、x+2、x+6、x+7、x+8、x+12、x+13、x+14,要求9个数之和,将这9个数加起来等于所给的数即可.
解答 解:观察图形可知,每个数比它下面的数小6,比它后边的小1.
∴设9个数中最小的一个为x,则可得出另外8个为x+1、x+2、x+6、x+7、x+8、x+12、x+13、x+14.
(1)框中9个数之和能为1998.
x+(x+1)+(x+2)+(x+6)+(x+7)+(x+8)+(x+12)+(x+13)+(x+14)=1998,
解得:x=215,即x+14=229,
∴框中9个数之和为1998,其中最小数是215,最大数是229;
(2)框中9个数之和不可能为2011.
理由:假设可以,
x+(x+1)+(x+2)+(x+6)+(x+7)+(x+8)+(x+12)+(x+13)+(x+14)=2011,
解得x=216.444…,不为整数,
故框中9个数之和不能为2011.
点评 此题考查数字的变化规律,找出数字在表格中的排列规律,利用数字之间的位置关系解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知一个直角三角形的两条边长恰好是方程x2-5x+6=0的两根,则它的第三条边长为( )
| A. | $\sqrt{13}$ | B. | 13 | C. | $\sqrt{13}$或$\sqrt{5}$ | D. | $\sqrt{13}$或3 |
18.已知A和B两点在线段EF的中垂线上,且∠EAF=100°,∠EBF=70°,则∠AEB等于( )
| A. | 95° | B. | 15° | C. | 95°或15° | D. | 170°或30° |
 如图,在?ABCD中,A、E、F共线,B、C、F共线,则与△FCE相似的三角形有2个.
如图,在?ABCD中,A、E、F共线,B、C、F共线,则与△FCE相似的三角形有2个.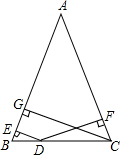 如图,已知△ABC中,AB=AC,D是底边BC上任意一点,DB=DC,DE⊥AB,DF⊥AC,CG⊥AB,求证:DE+DF=CG.
如图,已知△ABC中,AB=AC,D是底边BC上任意一点,DB=DC,DE⊥AB,DF⊥AC,CG⊥AB,求证:DE+DF=CG. 如图,△ABC中,DE∥BC,AN交DE于M,求证:$\frac{DM}{BN}=\frac{EM}{CN}$.
如图,△ABC中,DE∥BC,AN交DE于M,求证:$\frac{DM}{BN}=\frac{EM}{CN}$.