题目内容
12.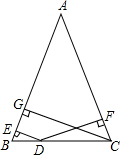 如图,已知△ABC中,AB=AC,D是底边BC上任意一点,DB=DC,DE⊥AB,DF⊥AC,CG⊥AB,求证:DE+DF=CG.
如图,已知△ABC中,AB=AC,D是底边BC上任意一点,DB=DC,DE⊥AB,DF⊥AC,CG⊥AB,求证:DE+DF=CG.
分析 作DM⊥CG于M,则∠DMG=∠DMC=90°,先证明四边形DMGE是矩形,得出DE=MG,DM∥AB,证出∠MDC=∠DCF,由AAS证明△DMC≌△CFD,得出MC=DF,即可得出结论.
解答 证明:作DM⊥CG于M,如图所示:
则∠DMG=∠DMC=90°,
∵DE⊥AB,DF⊥AC,CG⊥AB,
∴∠DEG=∠MGE=∠CFD=90°,
∴四边形DMGE是矩形,
∴DE=MG,DM∥AB,
∴∠MDC=∠B,
∵AB=AC,
∴∠B=∠DCF,
∴∠MDC=∠DCF,
在△DMC和△CFD中,
$\left\{\begin{array}{l}{∠DMC=∠CFD}&{\;}\\{∠MDC=∠DCF}&{\;}\\{DC=CD}&{\;}\end{array}\right.$,
∴△DMC≌△CFD(AAS),
∴MC=DF,
∵MG+MC=CG,
∴DE+DF=CG.
点评 本题考查了等腰三角形的性质、全等三角形的判定与性质、矩形的判定与性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
20.未来3到5年时间里,双流县将全力推进“四改六治理”各项工作,预计将完成130万平方米老住宅小区综合整治工作,130万这个数用科学记数法可表示为( )
| A. | 1.3×105 | B. | 1.3×106 | C. | 13×105 | D. | 13×106 |
7.用一个正方形框出9个数,要使这个正方形框出的9个数之和分别等于(1)1998(2)2011,这是否可能?若可能,求出框中最大数和最小数.若不可能,说明理由.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 |
| … | … | … | … | … | … |
| 997 | 998 | 999 | 1000 | 1001 | 1002 |
| … | … | … | … | … | … |

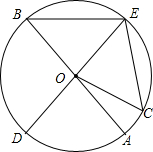 如图,AB,DE是⊙O的直径,C是⊙O上的一点,且$\widehat{AD}$=$\widehat{CE}$.
如图,AB,DE是⊙O的直径,C是⊙O上的一点,且$\widehat{AD}$=$\widehat{CE}$.