题目内容
18.已知直线l1∥l2,分别交l1、l2于A、B两点,点C在直线l2上且在点B的右侧,点D在直线l1上且在点A左侧,点P是直线l3上的动点,且不与A、B重合,设∠DAB=∠α.(1)如图1,当点P在线段AB上时,求证:∠APC=∠α+∠PCB;
(2)如图2,当点P在线段BA的延长线上时,请写出∠α、∠APC、∠PCB三个角之间的数量关系,并证明.
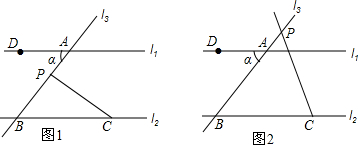
分析 (1)先根据平行线的性质得出∠α=∠PBC.再由∠APC是△PBC的一个外角得出∠APC=∠PBC+∠PCB,通过等量代换即可得出结论;
(2)由l1∥l2可知∠α=∠PBC,再根据三角形内角和定理得出∠PBC+∠PCB+∠APC=180°,利用等量代换即可得出结论.
解答 (1)证明:∵l1∥l2,
∴∠α=∠PBC.
∵∠APC是△PBC的一个外角,
∴∠APC=∠PBC+∠PCB,
∴∠APC=∠α+∠PCB.
(2)三个角的关系为:∠α+∠APC+∠PCB=180°.
证明:∵l1∥l2,
∴∠α=∠PBC.
∵∠PBC+∠PCB+∠APC=180°,
∴∠α+∠PCB+∠APC=180°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
相关题目
8.淮北市富强文体平价店以每件50元的价格购进800件某体育用品,第一个月以单价80元销售,售出了200件,第二个月如果单价不变,预计仍可售出200件,为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,将对剩余的体育用品一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)填表:(不需化简)
(2)如果该店希望通过销售这批体育用品获利9000元,那么第二个月的单价应是多少元?
(1)填表:(不需化简)
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(件) | 200 | 200+10x | 400-10x |
13. 如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )
如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )
 如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )
如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )| A. | L≤40.2 | B. | L≥39.98 | C. | 39.98≤L≤40.02 | D. | 39.8≤L≤40.2 |
7.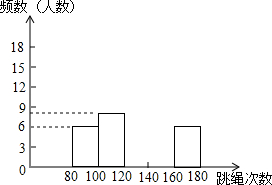 为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
请结合图表完成下列问题:
(1)求表中的a;
(2)请把频数分布直方图补充完整;
(3)若七年级学生一分钟跳绳次数(x)达标要求是:80≤x<120不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.为使合格率达到90%,至少还要将几人跳绳水平从不合格提高到合格或合格以上?
 为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:| 组 别 | 次 数x | 频数(人数) |
| 第一组 | 80≤x<100 | 6 |
| 第二组 | 100≤x<120 | 8 |
| 第三组 | 120≤x<140 | a |
| 第四组 | 140≤x<160 | 18 |
| 第五组 | 160≤x<180 | 6 |
(1)求表中的a;
(2)请把频数分布直方图补充完整;
(3)若七年级学生一分钟跳绳次数(x)达标要求是:80≤x<120不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.为使合格率达到90%,至少还要将几人跳绳水平从不合格提高到合格或合格以上?
 阅读下面的证明过程,在括号内补充推理的依据.
阅读下面的证明过程,在括号内补充推理的依据.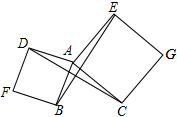 如图,以△ABC的两边AB、AC分别向外作正方形ABFD、ACGE,连接BE、DC,试猜测线段BE、DC的位置关系和数量关系,并说明理由.
如图,以△ABC的两边AB、AC分别向外作正方形ABFD、ACGE,连接BE、DC,试猜测线段BE、DC的位置关系和数量关系,并说明理由.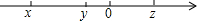 已知实数x、y、z在数轴上的对应点如图所示,化简:$\sqrt{(x-y)^{2}}$-($\sqrt{y-z}$)2+$\root{3}{(x-z)^{3}}$的值.
已知实数x、y、z在数轴上的对应点如图所示,化简:$\sqrt{(x-y)^{2}}$-($\sqrt{y-z}$)2+$\root{3}{(x-z)^{3}}$的值.