题目内容
12.若将正整数l、2、3、…98写在一起,则可以构成一个新的数字12345…91011…9798.(1)这个新数是一个几位数?
(2)这个新数各个数位上的数字之和为多少?
(3)在黑板上写上数l、2、3、…98,每次擦去任意的两个数,换上这两个数的和或差,重复这样的操作连续若干次,直到黑板上仅留下一个数为止,这个数是否可能为2016?请说明理由.
分析 (1)前面1到9,都是一位数,故有9位,后面接下来从10到98每个数都是两位,总共有(98-9)×2=89×2=178位数,所以1到98总共要178+9=187位数;
(2)前面1到9位数,是1到9的和,后面接下来是10个1的和,再接下来是0到9的和,再接下来是10个2的和,再接下来是0到9的和,…,最后是10个9的和以及0到9的和,所以各个位上的数字之间和为10(1+2+3+4+5+6+7+8+9)×2-9×2=882;
(3)根据两个数的和和两个数的差的奇偶性是相同的,所以若干次后剩余数的差和98个数的和的奇偶性相同,根据1、2、3、…98的和是(1+98)×98÷2=4851是奇数,2016不是奇数,所以没有这种可能性.
解答 解:(1)9+(98-9)×2
=9+178
=187,
所以,这个新数是一个187位数;
(2)10(1+2+3+4+5+6+7+8+9)×2-9×2
=10×45×2-18
=900-18
=882;
(3)由于两个数的和和两个数的差的奇偶性是相同的,
所以若干次后剩余数的差和98个数的和的奇偶性相同,
因为1+2+3+…+98=(1+98)×98÷2=4851是奇数,
2016不是奇数,所以没有这种可能性.
点评 本题考查了学生对数的构成、对大数的认识以及分析能力;两个数的和和两个数的差的奇偶性是相同的是解(3)的关键.

练习册系列答案
相关题目
17.由二次函数y=6(x-2)2+1,可知( )
| A. | 图象的开口向下 | B. | 图象的对称轴为直线x=$\frac{3}{2}$ | ||
| C. | 函数的最大值为1 | D. | 当x>2时,y随x的增大而增大 |
2.泸溪三口岩水库移民新村分给小慧家一套价格为12万元的住房,按要求,需首期(第一年)付房款3万元,从第二年起,每年应付房款0.5万元与上一年剩余房款的利息的和,假设剩余房款年利率为0.4%,小慧列表推算如下:
若第n年小慧家仍需还款,则第n年应还款0.54-0.002n万元(用含n的代数式表示,n>1).
| 第一年 | 第二年 | 第三年 | … | |
| 应还款(万元) | 3 | 0.5+9×0.4% | 0.5+8.5×0.4% | … |
| 剩余房款(万元) | 9 | 8.5 | 8 | … |
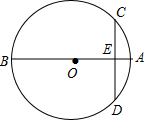 ⊙O的两条弦AB,CD相交于点E.
⊙O的两条弦AB,CD相交于点E.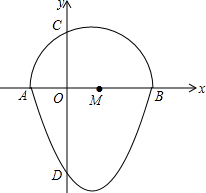 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.