题目内容
4.若两个相似三角形的面积比为1:9,则这两个相似三角形的周长比是1:3.分析 根据相似三角形面积的比等于相似比的平方求出相似比,根据相似三角形周长的比等于相似比解答即可.
解答 解:∵两个相似三角形的面积比为1:9,
∴这两个相似三角形的相似比为1:3,
∴这两个相似三角形的周长比1:3,
故答案为:1:3.
点评 本题考查的是相似三角形的性质,掌握相似三角形周长的比等于相似比、相似三角形面积的比等于相似比的平方是解题的关键.

练习册系列答案
相关题目
14.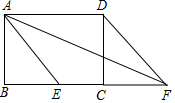 如图,矩形ABCD中,点E是BC边上一点,连接AE,将△ABE向右平移得到△DCF,连接AF.若四边形AEFD为菱形,AF=4$\sqrt{5}$,BE:EC=3:2,则AD长为( )
如图,矩形ABCD中,点E是BC边上一点,连接AE,将△ABE向右平移得到△DCF,连接AF.若四边形AEFD为菱形,AF=4$\sqrt{5}$,BE:EC=3:2,则AD长为( )
 如图,矩形ABCD中,点E是BC边上一点,连接AE,将△ABE向右平移得到△DCF,连接AF.若四边形AEFD为菱形,AF=4$\sqrt{5}$,BE:EC=3:2,则AD长为( )
如图,矩形ABCD中,点E是BC边上一点,连接AE,将△ABE向右平移得到△DCF,连接AF.若四边形AEFD为菱形,AF=4$\sqrt{5}$,BE:EC=3:2,则AD长为( )| A. | 3 | B. | $2\sqrt{3}$ | C. | 5 | D. | $2\sqrt{5}$ |
19.若二次函数y=x2+mx的对称轴是x=3,则抛物线y=x2+mx与x轴的交点坐标为( )
| A. | (0,0) | B. | (0,6) | C. | (0,0)和(0,6) | D. | (0,0)和(6,0) |
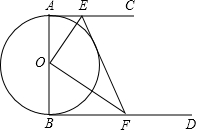 如图,AB是⊙O直径,AC、BD是⊙O的切线,切点分别为A、B,EF分别交AC、BD于点E、F,且EO平分∠AEF.
如图,AB是⊙O直径,AC、BD是⊙O的切线,切点分别为A、B,EF分别交AC、BD于点E、F,且EO平分∠AEF. 在Rt△ABC中,∠A=90°.
在Rt△ABC中,∠A=90°.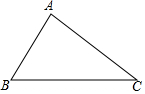 如图,已知△ABC,∠BAC=90°,请用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形(保留作图痕迹,不写作法)并说明理由.
如图,已知△ABC,∠BAC=90°,请用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形(保留作图痕迹,不写作法)并说明理由.