题目内容
20．△ABC中，∠ACB=120°，将它绕着点C逆时针旋转30°后得到△DCE，则∠ACE的度数为150°．分析 由旋转的性质得出∠DCE=∠ACB=120°，∠BCE=∠ACD=30°，即可得出结果．
解答 解：∵△ABC绕点C按逆时针方向旋转后得到△DEC，
∴∠DCE=∠ACB=120°，∠BCE=∠ACD=30°，
∴∠ACE=∠ACB+∠BCE=150°；
故答案为：150°．
点评 本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．
练习册系列答案
相关题目
11．若甲、乙、丙、丁四位射击运动员10次射击训练的平均成绩均为9.1环，方差分别为S甲2=0.80，S乙2=1.31，S丙2=1.72，S丁2=0.42，则成绩最稳定的运动员是（ ）
| A． | 甲 | B． | 乙 | C． | 丙 | D． | 丁 |
8．在下列关于x的函数中，一定是二次函数的是（ ）
| A． | y=x2 | B． | y=ax2+bx+c | C． | y=8x | D． | y=x2（1+x） |
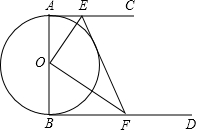如图，AB是⊙O直径，AC、BD是⊙O的切线，切点分别为A、B，EF分别交AC、BD于点E、F，且EO平分∠AEF．
在Rt△ABC中，∠A=90°．