题目内容
11.为了解都匀市交通拥堵情况,经统计分析,都匀彩虹桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为20辆/千米时,车流速度为80千米/小时.研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.(1)求彩虹桥上车流密度为100辆/千米时的车流速度;
(2)在交通高峰时段,为使彩虹桥上车流速度大于40千米/小时且小于60千米/小时,应控制彩虹桥上的车流密度在什么范围内?
(3)当车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.当20≤x≤220时,求彩虹桥上车流量y的最大值.
分析 (1)当20≤x≤220时,设车流速度v与车流密度x的函数关系式为v=kx+b,根据题意的数量关系建立方程组求出其解即可;
(2)由(1)的解析式建立不等式组求出其解即可;
(3)设车流量y与x之间的关系式为y=vx,当20≤x≤220时表示出函数关系,由函数的性质就可以求出结论.
解答 解:(1)设车流速度v与车流密度x的函数关系式为v=kx+b,由题意,得
$\left\{\begin{array}{l}{80=20k+b}\\{0=220k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{2}{5}}\\{b=88}\end{array}\right.$,
∴当20≤x≤220时,v=-$\frac{2}{5}$x+88,
当x=100时,v=-$\frac{2}{5}$×100+88=48(千米/小时);
(2)由题意,得
$\left\{\begin{array}{l}{-\frac{2}{5}x+88>40}\\{-\frac{2}{5}x+88<60}\end{array}\right.$,
解得:70<x<120,
∴应控制大桥上的车流密度在70<x<120范围内;
(3)设车流量y与x之间的关系式为y=vx,
当20≤x≤220时,
y=(-$\frac{2}{5}$x+88)x=-$\frac{2}{5}$(x-110)2+4840,
∴当x=110时,y最大=4840,
∵4840>1600,
∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆.
点评 本题考查了车流量=车流速度×车流密度的运用,一次函数的解析式的运用,一元一次不等式组的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案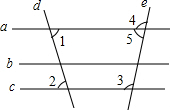 如图,下列说法错误的是( )
如图,下列说法错误的是( )| A. | 若a∥b,b∥c,则a∥c | B. | 若∠1=∠2,则a∥c | ||
| C. | 若∠3=∠2,则b∥c | D. | 若∠3+∠5=180°,则a∥c |
| A. | $\sqrt{\frac{-4}{-9}}$=$\frac{\sqrt{-4}}{\sqrt{-9}}$=$\frac{-2}{-3}$=$\frac{2}{3}$ | B. | $\sqrt{4\frac{2}{9}}$=$\sqrt{\frac{38}{9}}$=2$\frac{1}{3}$$\sqrt{2}$ | ||
| C. | $\sqrt{\frac{3}{7}}$÷$\sqrt{3\frac{1}{2}}$=$\frac{\sqrt{6}}{7}$ | D. | $\sqrt{\frac{8}{25}}$=5$\sqrt{8}$ |
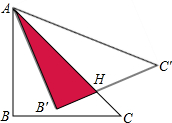 如图,等腰直角三角形ABC的直角边AB的长为6cm,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点H,则图中△AHC′的面积等于( )
如图,等腰直角三角形ABC的直角边AB的长为6cm,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点H,则图中△AHC′的面积等于( )| A. | 12-6$\sqrt{3}$ | B. | 14-6$\sqrt{3}$ | C. | 18-6$\sqrt{3}$ | D. | 18+6$\sqrt{3}$ |
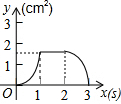
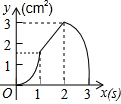
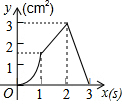
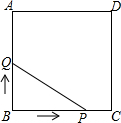 如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )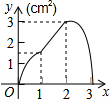
 如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=360°.
如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=360°.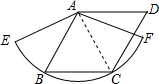 如图,边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上.若∠BAD=120°,则弧BC的长度等于$\frac{π}{3}$(结果保留π).
如图,边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上.若∠BAD=120°,则弧BC的长度等于$\frac{π}{3}$(结果保留π).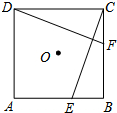 如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转的角度为90°.
如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转的角度为90°.