题目内容
2. 如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=360°.
如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=360°.
分析 首先根据图示,可得∠1=180°-∠BAE,∠2=180°-∠ABC,∠3=180°-∠BCD,∠4=180°-∠CDE,∠5=180°-∠DEA,然后根据三角形的内角和定理,求出五边形ABCDE的内角和是多少,再用180°×5减去五边形ABCDE的内角和,求出∠1+∠2+∠3+∠4+∠5等于多少即可.
解答 解:∠1+∠2+∠3+∠4+∠5
=(180°-∠BAE)+(180°-∠ABC)+(180°-∠BCD)+(180°-∠CDE)+(180°-∠DEA)
=180°×5-(∠BAE+∠ABC+∠BCD+∠CDE+∠DEA)
=900°-(5-2)×180°
=900°-540°
=360°.
故答案为:360°.
点评 此题主要考查了多边形内角和定理,要熟练掌握,解答此题的关键是要明确:(1)n边形的内角和=(n-2)•180 (n≥3)且n为整数).(2)多边形的外角和指每个顶点处取一个外角,则n边形取n个外角,无论边数是几,其外角和永远为360°.

练习册系列答案
相关题目
14.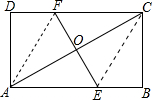 如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则$\frac{AE}{EB}$等于( )
如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则$\frac{AE}{EB}$等于( )
 如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则$\frac{AE}{EB}$等于( )
如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则$\frac{AE}{EB}$等于( )| A. | $\sqrt{3}$ | B. | 2 | C. | 1.5 | D. | $\sqrt{2}$ |
1.已知反比例函数y=-$\frac{3}{x}$,下列结论不正确的是( )
| A. | 图象必经过点(-1,3) | B. | 若x>1,则-3<y<0 | ||
| C. | 图象在第二、四象限内 | D. | y随x的增大而增大 |
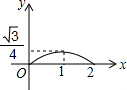
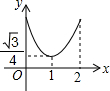
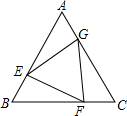 如图,已知正△ABC的边长为2,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )
如图,已知正△ABC的边长为2,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )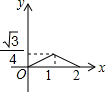
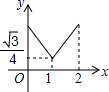
 如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于5π.
如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于5π.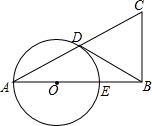 已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.



 在?ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.
在?ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.