��Ŀ����
5������̽������֪����ABCD�У�AB=4��BC=5����E��F�ֱ���AD��AB��һ���㣬�۵�����ABCD����A1Ϊ��A�Ķ�Ӧ�㣮��1����ͼ1����ֱ��EF�۵�����ABCD����A1�Ǿ���ABCD��һ�㣬��������A1EF��Ҫ�߹���ͼ��������ͼ�ۼ�����д��������
��2����ͼ2����ֱ��BE�۵�����ABCD����A�Ķ�Ӧ��A1ǡ�����ڡ�BCD��ƽ������ʱ����CA1�ij���
��չ���죺
��3��ȥ����BC=5��������������ֱ��BE�۵����κ����ڡ�BCDƽ�����ϵĵ�A1����ֻ��һ��ʱ������ε������
��4���Ѿ���ABCD��ֱ��EF�۵���A�Ķ�Ӧ��A1���ھ���ABCD�ڣ���������Ե���֣���ֱ��д��DA1����Сֵ��

���� ��1���ֱ���A��A1ΪԲ�ģ�����AA1����һ��Ϊ�뾶��������������M��N���㣬��ֱ��MN����AD��E����AB��F������A1E��A1F�����A1EF��Ϊ����
��2������A1��A1F��BC��F����A1F=CF=x����BF=5-x����Rt��A1BF�У����ݹ��ɶ����ó�A1F2+BF2=A1B2�������õ�x2+��5-x��2=42�����CF=$\frac{5+\sqrt{7}}{2}$��$\frac{5-\sqrt{7}}{2}$��������ڵ���Rt��A1CF�У����CA1���ɣ�
��3������B����BCD��ƽ���ߵĴ��ߣ�����A1���ڴ�����ʱ����A1����ֻ��һ�������ݡ�A1BC�ǵ���ֱ�������Σ��õ�A1B=A1C=4�����BC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$���ݴ���þ��ε������
��4����������֮���߶���̣��Լ�A1B=AB=4�ɵã�����B��A1��D���㹲��ʱ��A1D��̣���Rt��ABD�У����ݹ��ɶ������BD�ij������ɵõ�DA1����Сֵ��
��� �⣺��1����ͼ1��ʾ���ֱ���A��A1ΪԲ�ģ�����AA1����һ��Ϊ�뾶��������������M��N���㣬��ֱ��MN����AD��E����AB��F������A1E��A1F�����A1EF��Ϊ����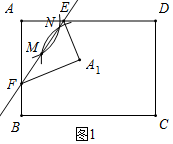
��2����ͼ2��ʾ������A1��A1F��BC��F��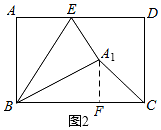
�ߵ�A1���ڡ�BCD��ƽ�����ϣ�
���BCA1=45�㣬
���A1CF�ǵ���ֱ�������Σ�
��A1F=CF=x����BF=5-x��
���۵��ɵã�A1B=AB=4��
��Rt��A1BF��A1F2+BF2=A1B2��
��x2+��5-x��2=42��
���x1=$\frac{5+\sqrt{7}}{2}$��x2=$\frac{5-\sqrt{7}}{2}$��
��CF=$\frac{5+\sqrt{7}}{2}$��$\frac{5-\sqrt{7}}{2}$��
���ڵ���Rt��A1CF�У�CA1=$\sqrt{2}$CF=$\frac{5}{2}\sqrt{2}$+$\frac{\sqrt{14}}{2}$��$\frac{5}{2}\sqrt{2}$-$\frac{\sqrt{14}}{2}$��
��3����ͼ3��ʾ������B����BCD��ƽ���ߵĴ��ߣ�����A1���ڴ�����ʱ����A1����ֻ��һ����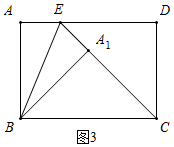
��ʱ����A1BC�ǵ���ֱ�������Σ�
��A1B=A1C=4��
��BC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$��
�������=4��4$\sqrt{2}$=16$\sqrt{2}$��
��4����ͼ4��ʾ����������֮���߶���̣��Լ�A1B=AB=4�ɵã�
����B��A1��D���㹲��ʱ��A1D��̣�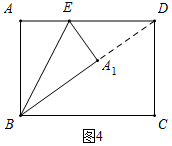
��ʱ��Rt��ABD�У�BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{4}^{2}+{5}^{2}}$=$\sqrt{41}$��
��A1D=$\sqrt{41}$-4��
��DA1����СֵΪ$\sqrt{41}$-4��
���� ���������ı����ۺ��⣬��Ҫ�����˾��ε����ʣ�����ֱ�������ε����ʣ���ԳƵ����ʣ���һԪ���η����Լ����ɶ������ۺ�Ӧ�ã��������Ĺؼ������գ��۵���һ�ֶԳƱ任����������Գƣ��۵�ǰ��ͼ�ε���״�ʹ�С���䣬λ�ñ仯����Ӧ�ߺͶ�Ӧ����ȣ�����ʱע�⣺��Ҫ����߶γ�Ϊx��Ȼ������۵�����ԳƵ������ú�x�Ĵ���ʽ��ʾ�����߶εij��ȣ�ѡ���ʵ���ֱ�������Σ����ù��ɶ����г����̼�������𰸣�

 ��1���ⷽ�̣�x��x-2��+x-2=0
��1���ⷽ�̣�x��x-2��+x-2=0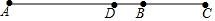 ��ͼ����֪�߶�AB�ij�Ϊa���ӳ��߶�AB����C��ʹBC=$\frac{1}{2}$AB��
��ͼ����֪�߶�AB�ij�Ϊa���ӳ��߶�AB����C��ʹBC=$\frac{1}{2}$AB��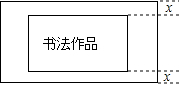 ��ͼ������һ���鷨��Ʒ��ͼ����Ӱ������ʾ����Ҫװ�ѣ���֪���鷨��Ʒ�ij�Ϊ50cm����Ϊ30cm���ϡ��±߳ĵȿ������ұ߳ĵȿ��������ϡ��±߳ĵĿ������ұ߳ĵĿ���Ϊ1��2����֪װ�Ѻ����Ʒ�����Ϊ2800cm2��
��ͼ������һ���鷨��Ʒ��ͼ����Ӱ������ʾ����Ҫװ�ѣ���֪���鷨��Ʒ�ij�Ϊ50cm����Ϊ30cm���ϡ��±߳ĵȿ������ұ߳ĵȿ��������ϡ��±߳ĵĿ������ұ߳ĵĿ���Ϊ1��2����֪װ�Ѻ����Ʒ�����Ϊ2800cm2��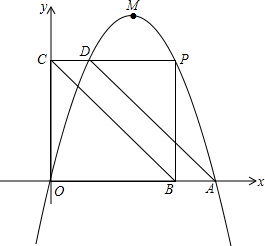 ��ƽ��ֱ������ϵxOy�У�������y=-x2+4x��x��������ύ�ڵ�A���䶥��ΪM����P�Ǹ���������λ��A��M����֮��IJ����ϵĶ��㣬����P��PB��x���ڵ�B��PC��y���ڵ�C���ҽ��������ڵ�D������BC��AD��OP�����ı���ABCD��OP�ֳɵ������������Ϊ1��2ʱ����P������Ϊ��$\frac{12}{5}$��$\frac{96}{25}$����
��ƽ��ֱ������ϵxOy�У�������y=-x2+4x��x��������ύ�ڵ�A���䶥��ΪM����P�Ǹ���������λ��A��M����֮��IJ����ϵĶ��㣬����P��PB��x���ڵ�B��PC��y���ڵ�C���ҽ��������ڵ�D������BC��AD��OP�����ı���ABCD��OP�ֳɵ������������Ϊ1��2ʱ����P������Ϊ��$\frac{12}{5}$��$\frac{96}{25}$����