Question

1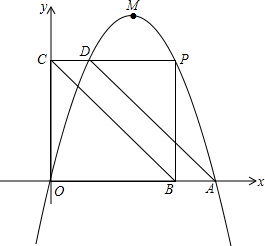．在平面直角坐标系xOy中，抛物线y=-x²+4x与x轴的正半轴交于点A，其顶点为M，点P是该抛物线上位于A、M两点之间的部分上的动点，过点P作PB⊥x轴于点B，PC⊥y轴于点C，且交抛物线于点D，连接BC，AD，OP，当四边形ABCD被OP分成的两部分面积比为1：2时，点P的坐标为（$\frac{12}{5}$，$\frac{96}{25}$）．

Answer 1

分析 如图，连接OP交BC于E，交AD于F．首先证明四边形OCPB是矩形，四边形ABCD是平行四边形，BC=AD，设EC=EB=a，DF=x，平行四边形BC边上的高为h，则BC=AD=2a，AF=2a-x，由题意，$\frac{1}{2}$（a+x）h：$\frac{1}{2}$（a+2a-x）h=2：1或$\frac{1}{2}$（a+x）h：$\frac{1}{2}$（a+2a-x）h=1：2，解得x=$\frac{5}{3}a$或$\frac{1}{3}$a，推出DF：AF=1：5或5：1，求出PD的长，设C（0，m），由$\left\{\begin{array}{l}{y=m}\\{y=-{x}^{2}+4x}\end{array}\right.$消去y得到，x²-4x+m=0，设两根为x₁，x₂，由题意|x₁-x₂|=$\frac{4}{5}$，得到（x₁+x₂）²-4x₁x₂=$\frac{16}{25}$，可得16-4m=$\frac{16}{25}$，求出m，再求出方程的根即可．

解答 解：如图，连接OP交BC于E，交AD于F．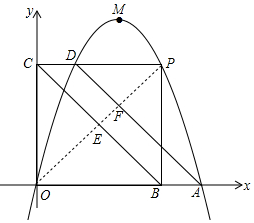

∵∠PCO=∠COB=∠PBO=90°，
∴四边形OCPB是矩形，
∴EC=EB，PC∥OB，
根据对称性可知，CD=AB，四边形ABCD是平行四边形，
∴BC=AD，设EC=EB=a，DF=x，平行四边形BC边上的高为h，则BC=AD=2a，AF=2a-x，
由题意，$\frac{1}{2}$（a+x）h：$\frac{1}{2}$（a+2a-x）h=2：1或$\frac{1}{2}$（a+x）h：$\frac{1}{2}$（a+2a-x）h=1：2，
∴x=$\frac{5}{3}a$或$\frac{1}{3}$a，
∴DF：AF=1：5或5：1
∵DP∥OA，
∴$\frac{DP}{OA}$=$\frac{DF}{AF}$=$\frac{1}{5}$或5，
∵OA=4，
∴DP=$\frac{4}{5}$或20（舍弃），
设C（0，m），
由$\left\{\begin{array}{l}{y=m}\\{y=-{x}^{2}+4x}\end{array}\right.$消去y得到，x²-4x+m=0，设两根为x₁，x₂，
∴|x₁-x₂|=$\frac{4}{5}$，
∴（x₁+x₂）²-4x₁x₂=$\frac{16}{25}$，
∴16-4m=$\frac{16}{25}$，
∴m=$\frac{96}{25}$，
∴x²-4x+$\frac{96}{25}$=0，
∴x₁=$\frac{12}{5}$或$\frac{8}{5}$，
∴点P坐标（$\frac{12}{5}$，$\frac{96}{25}$），
故答案为（$\frac{12}{5}$，$\frac{96}{25}$）．

点评 本题考查二次函数的应用，矩形的判定和性质、平行四边形的判定和性质、一元二次方程的根与系数的关系等知识，解题的关键是灵活运用所学知识，属于中考填空题中的压轴题．