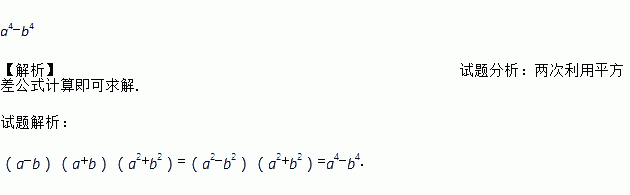题目内容
(a-b)(a+b)(a2+b2)
 a4-b4
【解析】试题分析:两次利用平方差公式计算即可求解.
试题解析:
(a-b)(a+b)(a2+b2)=(a2-b2)(a2+b2)=a4-b4.
a4-b4
【解析】试题分析:两次利用平方差公式计算即可求解.
试题解析:
(a-b)(a+b)(a2+b2)=(a2-b2)(a2+b2)=a4-b4.
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( )

A.2 B.3 C.4 D.5
 D
【解析】
根据等腰三角形的性质可得AB=AC,继而得出AC的长.
【解析】
∵∠B=∠C,
∴AB=AC=5.
故选D.
D
【解析】
根据等腰三角形的性质可得AB=AC,继而得出AC的长.
【解析】
∵∠B=∠C,
∴AB=AC=5.
故选D. (3a-b)(3a+b)-(2a-b)2
 5a2+4ab-2b2
【解析】试题分析:先根据平方差公式与完全平方公式分别计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(2a-b)2=9a2-b2-4a2+4ab-b2=5a2+4ab-2b2.
5a2+4ab-2b2
【解析】试题分析:先根据平方差公式与完全平方公式分别计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(2a-b)2=9a2-b2-4a2+4ab-b2=5a2+4ab-2b2. (2y-3z)2 等于( )
A. 4y2-12yz+z2 B. .y2-12yz+9z2 C. 4y2-12yz+9z2 D. .4y2-6yz+9z2
 C
【解析】根据完全平方公式可得:(2y-3z)2=4y2-12yz+9z2,故选C.
C
【解析】根据完全平方公式可得:(2y-3z)2=4y2-12yz+9z2,故选C. (2x-1)2等于( )
A. 4x2-4x+1 B. 2x2-2x+1 C. 2x2-1 D. 2x2+1
 A
【解析】根据完全平方公式可得:(2x-1)2=4x2-4x+1 ,故选A.
A
【解析】根据完全平方公式可得:(2x-1)2=4x2-4x+1 ,故选A. (5+x2)(5-x2)等于_______;
 25-x4
【解析】根据平方差公式可得:(5-x2)(5-x2)=25-x4.
25-x4
【解析】根据平方差公式可得:(5-x2)(5-x2)=25-x4. (y+3z)(3z-y)等于( )
A. y2-z2 B. y2-9z2 C. 9z2-y2 D. y2-z2
 C
【解析】根据平方差公式可得:(y+3z)(3z-y)=9z2-y2,故选C.
C
【解析】根据平方差公式可得:(y+3z)(3z-y)=9z2-y2,故选C. 如图,点A2,A4…分别是x轴上的点,点A1,A3,A5,…分别是射线OA2n-1上的点,△OA1A2,△OA2A3,△OA3A4,…分别是以OA2,OA3,OA4 ,OA5…为底边的等腰三角形,若OA2n-1与x轴正半轴的夹角为30°,OA1=1,则可求得点A2的坐标是________;A2n-1的坐标_______.
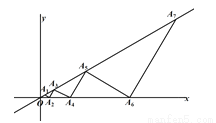
 【解析】根据等腰三角形的三线合一的性质和30°角直角三角形的性质可求得, ,再由等腰三角形的三线合一的性质和30°角直角三角形的性质可求得, ,由此可得A2n-1的坐标.
【解析】根据等腰三角形的三线合一的性质和30°角直角三角形的性质可求得, ,再由等腰三角形的三线合一的性质和30°角直角三角形的性质可求得, ,由此可得A2n-1的坐标. 使分式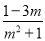 的值为非负数的
的值为非负数的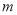 的取值范围是( )
的取值范围是( )
A. 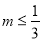 B.
B. 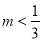 C.
C. 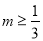 D.
D. 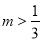
 A
【解析】根据分式的分母的最小值为1,分式值为非负数,得到分子大于等于0,即可求出m的范围.
【解析】
∵?0,且m2+1?1,
∴1?3m?0,
解得:m?.
故选A.
A
【解析】根据分式的分母的最小值为1,分式值为非负数,得到分子大于等于0,即可求出m的范围.
【解析】
∵?0,且m2+1?1,
∴1?3m?0,
解得:m?.
故选A.