Question

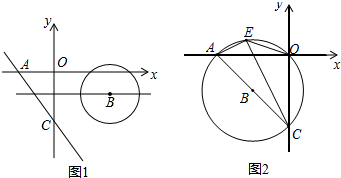
如图1，在平面直角坐标系中，直线α：y=-x-

2

与坐标轴分别交于A，C两点，
（1）求点A的坐标及∠CAO的度数；
（2）点B为直线y=-

2

2

上的一个动点，以点B为圆心，AC长为直径作⊙B，当⊙B与直线α相切时，求B点的坐标；
（3）如图2，当⊙B过A，O，C三点时，点E是劣弧上一点，连接EC，EA，EO，当点E在劣弧上运动时（不与A，O两点重合），

EC-EA

EO

的值是否发生变化？如果不变，求其值，如果变化，说明理由．

Answer 1

考点：圆的综合题

专题：

分析：（1）已知点A，C的坐标，故可推出OA=OC，最后可得∠CAO=45°．
（2）设B（m，-

2

2

）．依题意，由于直线BM的斜率为1，则设直线BM为：y=x+b，代入B求得直线BM的解析式，解两个解析式构成的方程组求得交点M的坐标，然后根据BM等于圆B的半径，列出方程，解这个方程即可求得；
（3）在CE上截取CK=EA，连接OK，证明△OAE≌△OCK推出OE=OK，∠EOA=∠KOC，∠EOK=∠AOC=90°．最后可证明

EC-EA

EO

=

2

．

解答：解：（1）令直线a：y=-x-

2

中，y=0求出x=-

2

，
∴A（-

2

，0），
令x=0求出y=-

2

，∴C（0，-

2

），
∴OA=OC，
∵OA⊥OC，
∴△AOC为等腰直角三角形，
∴∠CAO=45°；

（2）如图1，设B（m，-

2

2

）．
∵⊙B与直线α相切，
∴BM⊥AC，
∴直线BM的斜率为1，
∴设直线BM为：y=x+b，
代入B点的坐标得：b=-m-

2

2

，
∴直线BM的解析式为：y=x-m-

2

2

，
解

y=x-m- 2 2 y=-x- 2

得：

x= m 2 - 2 4 y=- m 2 - 3 2 4

，
∴交点M（

m

2

-

2

4

，-

m

2

-

3 2

4

），
∴（

m

2

-

2

4

-m）²+（-

m

2

-

3 2

4

+

2

2

）²=（

2

2

）²
解得：m=

2

2

或m=-

3 2

2

，
∴B（

2

2

，-

2

2

）或（-

3 2

2

，-

2

2

）；

（3）

EC-EA

EO

的值不变，等于

2

，如图2，
在CE上截取CK=EA，连接OK，
∵∠OAE=∠OCK，OA=OC，
∴△OAE≌△OCK，
∴OE=OK，∠EOA=∠KOC，
∴∠EOK=∠AOC=90°，
∴EK=

2

EO，∴

EC-EA

EO

=

2

．

点评：此题综合考查了点的坐标的求法、函数、图形的平移与旋转、圆的有关性质等知识．此题综合性强，难度较大，把重点知识穿插进行了考查．