题目内容
计算:
(1)20092-2010×2008;
(2)(-2)0-|-5|+(-
)-2+22011×(-
)2011.
(1)20092-2010×2008;
(2)(-2)0-|-5|+(-
| 1 |
| 2 |
| 1 |
| 2 |
考点:整式的混合运算,零指数幂,负整数指数幂
专题:
分析:(1)把2010×2008变形为(2009+1)×(2009-1),进一步利用平方差公式计算即可;
(2)先算0指数幂、负整数指数幂、绝对值与积的乘方,再算乘法,最后算加减即可.
(2)先算0指数幂、负整数指数幂、绝对值与积的乘方,再算乘法,最后算加减即可.
解答:解:(1)原式=20092-(2009+1)×(2009-1)
=20092-(20092-1)
=20092-20092+1
=1;
(2)原式=1-5+4+[2×(-
)]2011
=1-5+4-1
=-1.
=20092-(20092-1)
=20092-20092+1
=1;
(2)原式=1-5+4+[2×(-
| 1 |
| 2 |
=1-5+4-1
=-1.
点评:此题考查整式的混合运算,掌握平方差公式和整式的乘法法则是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
化简(x+3)(x-3)-x(x-2)的结果为( )
| A、-2x-9 | B、-2x+9 |
| C、2x-9 | D、2x+9 |
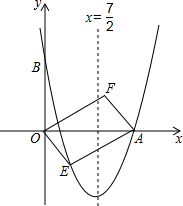 如图,对称轴为直线x=
如图,对称轴为直线x=
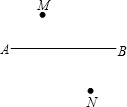 如图,一辆汽车在笔直的公路AB上由A向B行驶,M、N分别是位于公路AB两侧的村庄.设汽车行驶到点P时,离村庄M最近,汽车行驶到点Q时,离村庄N最近,汽车行驶到点O时,离村庄M、N的距离和最小,请在图中公路AB上分别画出点P、Q、O的位置,并简要说明数学原理.
如图,一辆汽车在笔直的公路AB上由A向B行驶,M、N分别是位于公路AB两侧的村庄.设汽车行驶到点P时,离村庄M最近,汽车行驶到点Q时,离村庄N最近,汽车行驶到点O时,离村庄M、N的距离和最小,请在图中公路AB上分别画出点P、Q、O的位置,并简要说明数学原理.