Question

5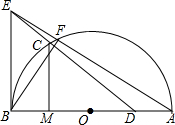．如图，在半径为2的⊙O中，AB是直径，C是弧AB的三等分点（∠BOC为锐角），D是OA的中点，BE是⊙O的切线，B为切点，DC的延长线交BE于点E，连接AE，交⊙O于点F．
（1）求∠BOC的度数；
（2）作CM⊥AB，垂足为M，连接BF，分别求CM，BF的长．

Answer 1

分析 （1）根据同弧所对的圆心角相等，即可解答；
（2）根据锐角三角函数，求出CM，OM的值，根据两角相等的三角形相似，证得△DMC∽△DBE，进而求得BE的值，根据勾股定理求出AE的值，再利用面积法求出BF的长度即可．

解答 解：（1）如图，连接OC，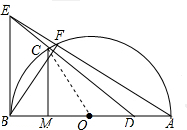
∵C是弧AB的三等分点，
∴∠BOC=$\frac{1}{3}$×180°=60°；
（2）在Rt△OMC中，OC=2，∠COM=60°，
∴CM=sin60°×OC=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$，OM=cos60°×OC=$\frac{1}{2}$×2=1，
∵BE是切线，
∴∠ABE=90°，
∵CM⊥AB，
∴∠CMO=90°=∠ABE，
∴△DMC∽△DBE，
∴$\frac{DM}{DB}=\frac{CM}{BE}$，即$\frac{2}{3}=\frac{\sqrt{3}}{BE}$，解得：BE=$\frac{3\sqrt{3}}{2}$，
在Rt△ABE中，AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{4}^{2}+（\frac{3\sqrt{3}}{2}）^{2}}$=$\frac{\sqrt{91}}{2}$，
∵AB是直径，
∴∠AFB=90°，
∵${S}_{△ABE}=\frac{1}{2}•BF•AE=\frac{1}{2}BE•AB$，
∴BF=$\frac{BE•AB}{AE}$=$\frac{\frac{3\sqrt{3}}{2}×4}{\frac{\sqrt{91}}{2}}$=$\frac{12\sqrt{273}}{91}$．

点评 本题主要考查切线的性质，相似的性质与判定，勾股定理等的综合应用，此题难度适中，能够想到利用三角形相似的性质和勾股定理求出相关线段的长度是解决此题的关键．