题目内容
已知点A(x1,y1)、B(x2,y2)在二次函数y=(x-1)2+1的图象上,若x1-x2=4,则当x1= 时,y1=y2.
考点:二次函数图象上点的坐标特征
专题:
分析:根据y1=y2列出方程,根据x1-x2=4得出x2=x1-4通过代换得出关于x1方程,解方程即可;
解答:解:∵点A(x1,y1)、B(x2,y2)在二次函数y=(x-1)2+1的图象上,
∴y1=(x1-1)2+1,y2=(x2-1)2+1,
∵y1=y2,
∴(x1-1)2+1=(x2-1)2+1,
∵x1-x2=4,
∴x2=x1-4,
∴(x1-1)2=(x1-5)2,
∴x1-1=-(x1-5),
解得,x1=3,
故答案为3;
∴y1=(x1-1)2+1,y2=(x2-1)2+1,
∵y1=y2,
∴(x1-1)2+1=(x2-1)2+1,
∵x1-x2=4,
∴x2=x1-4,
∴(x1-1)2=(x1-5)2,
∴x1-1=-(x1-5),
解得,x1=3,
故答案为3;
点评:本题考查了二次函数图象上点的坐标特征,主要通过解方程求得x1的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=36°,则∠C的度数为( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=36°,则∠C的度数为( )| A、18° | B、27° |
| C、36° | D、54° |
 如图,AD是△ABC的中线,DE⊥AB于点E,DF⊥AC于F,且BE=CF,问AD是否平分∠BAC,如果是,请说明理由.
如图,AD是△ABC的中线,DE⊥AB于点E,DF⊥AC于F,且BE=CF,问AD是否平分∠BAC,如果是,请说明理由.
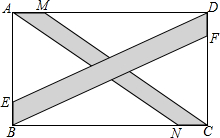 如图,在矩形ABCD中,点E、F在AB、CD上,BF∥DE,若AD=12,AB=7,且AE:EB=5:2,又有点M,N也在AD、BC上,且AM:MD=1:5,AN∥MC,求S空白.
如图,在矩形ABCD中,点E、F在AB、CD上,BF∥DE,若AD=12,AB=7,且AE:EB=5:2,又有点M,N也在AD、BC上,且AM:MD=1:5,AN∥MC,求S空白.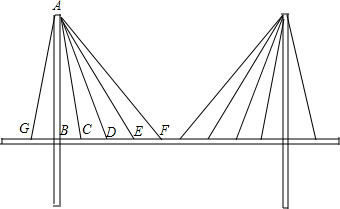 二次根式的加减在日常生活中有着广泛的应用.如在一座斜拉桥上可以看到很多拉索.如图所示,事实上,AB⊥GF.若AB=24m,BC=2m,BC=CD=DE=EF,桥的两个立柱两边各拉4条这样的拉索,那么拉索的总长度是多少米?
二次根式的加减在日常生活中有着广泛的应用.如在一座斜拉桥上可以看到很多拉索.如图所示,事实上,AB⊥GF.若AB=24m,BC=2m,BC=CD=DE=EF,桥的两个立柱两边各拉4条这样的拉索,那么拉索的总长度是多少米?