题目内容
 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=36°,则∠C的度数为( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=36°,则∠C的度数为( )| A、18° | B、27° |
| C、36° | D、54° |
考点:切线的性质
专题:
分析:连接OB,根据切线的性质得到OB⊥AB,求出∠OBA=90°,根据三角形的内角和定理求出∠AOB的度数,由∠C和∠AOB是同弧所对的圆周角和圆心角,根据圆周角定理即可求出∠C.
解答:解:连接OB,
∵AB切圆O于B,
∴OB⊥AB,
∴∠OBA=90°,
∵∠A=36°,
∴∠AOB=180°-∠A-∠OBA=54°,
∵∠C和∠AOB是同弧所对的圆周角和圆心角,
∴∠C=
∠AOB=27°.
故选B.

∵AB切圆O于B,
∴OB⊥AB,
∴∠OBA=90°,
∵∠A=36°,
∴∠AOB=180°-∠A-∠OBA=54°,
∵∠C和∠AOB是同弧所对的圆周角和圆心角,
∴∠C=
| 1 |
| 2 |
故选B.
点评:本题主要考查对三角形的内角和定理,垂线的定义,圆周角定理,切线的性质等知识点的理解和掌握,能灵活运用切线的性质和圆周角定理进行推理是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列图形中,能够折叠成正方体的是( )
A、 |
B、 |
C、 |
D、 |
设计调查问卷时要注意( )
①问题应尽量简明;②不要提问被调查者不愿意回答的问题;③提问不能涉及提问者的个人观点;④提供的选择答案要尽可能全面;⑤问卷应简洁.
①问题应尽量简明;②不要提问被调查者不愿意回答的问题;③提问不能涉及提问者的个人观点;④提供的选择答案要尽可能全面;⑤问卷应简洁.
| A、①②④⑤ | B、①③④⑤ |
| C、①②③④⑤ | D、①⑤ |
 如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.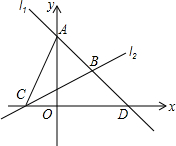 如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点;一次函数y=
如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点;一次函数y= 抛物线y=ax2+bx+c的部分图象如图所示,则关于x的不等式ax2+bx+c+2>0的解集为
抛物线y=ax2+bx+c的部分图象如图所示,则关于x的不等式ax2+bx+c+2>0的解集为