题目内容
请你用所学的知识,在下面两项中任选其一作图.
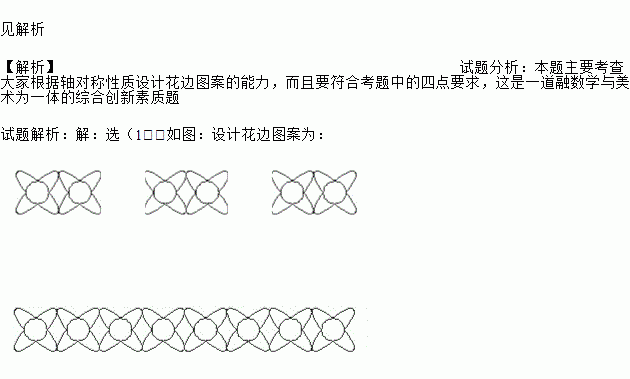
(1)参考下图,为班级的黑板报设计一组花边图案.

(2)以三角形、矩形、圆形为“基本图案”通过平移、旋转、轴对称为班级设计一个班徽.
 见解析
【解析】试题分析:本题主要考查大家根据轴对称性质设计花边图案的能力,而且要符合考题中的四点要求,这是一道融数学与美术为一体的综合创新素质题
试题解析:【解析】
选(1).如图:设计花边图案为:
见解析
【解析】试题分析:本题主要考查大家根据轴对称性质设计花边图案的能力,而且要符合考题中的四点要求,这是一道融数学与美术为一体的综合创新素质题
试题解析:【解析】
选(1).如图:设计花边图案为:
练习册系列答案
相关题目
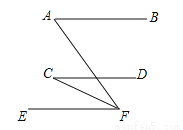
如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数是( )
A.25° B.35° C.45° D.50°
 D.
【解析】
试题分析:∵CD∥EF,∠C=∠CFE=25°,∵FC平分∠AFE,∴∠AFE=2∠CFE=50°,又∵AB∥EF,∴∠A=∠AFE=50°,故选D.
D.
【解析】
试题分析:∵CD∥EF,∠C=∠CFE=25°,∵FC平分∠AFE,∴∠AFE=2∠CFE=50°,又∵AB∥EF,∴∠A=∠AFE=50°,故选D. 已知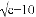 +|a-6|+(b-8)2=0,则以a、b、c为三边的三角形是__________.
+|a-6|+(b-8)2=0,则以a、b、c为三边的三角形是__________.
 直角三角形
【解析】【解析】
∵,∴a-6=0, b-8=0,c-10=0,∴a=6,b=8,c=10,
∴a2+b2=c2,∴以a、b、c为三边的三角形是直角三角形.故答案为:直角.
直角三角形
【解析】【解析】
∵,∴a-6=0, b-8=0,c-10=0,∴a=6,b=8,c=10,
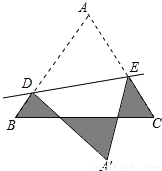
∴a2+b2=c2,∴以a、b、c为三边的三角形是直角三角形.故答案为:直角. 如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为_______cm.
 3
【解析】因为等边三角形ABC的边长为1cm,
所以AB=BC=AC=1cm,
因为△ADE沿直线DE折叠,点A落在点F处,
所以AD=FD,AE=FE,
所以阴影部分图形的周长为:
BD+FD+BC+FE+EC=BD+AD+BC+AE+EC=AB+BC+AC=1+1+1=3(cm)
故答案为:3.
3
【解析】因为等边三角形ABC的边长为1cm,
所以AB=BC=AC=1cm,
因为△ADE沿直线DE折叠,点A落在点F处,
所以AD=FD,AE=FE,
所以阴影部分图形的周长为:
BD+FD+BC+FE+EC=BD+AD+BC+AE+EC=AB+BC+AC=1+1+1=3(cm)
故答案为:3. 在△ABC中,AB=AC,若∠A=40°,则∠B=__________度.
 70
【解析】∵AB=AC,
∴∠B=∠C,
∵∠A=40°,
∴∠B=∠C=(180?40)=70°,
故答案为:70.
70
【解析】∵AB=AC,
∴∠B=∠C,
∵∠A=40°,
∴∠B=∠C=(180?40)=70°,
故答案为:70. 为了美化绿地,要在给定的一块长方形的空地上设计一个花坛,只允许用正方形和圆两种图形,并使整个图案成轴对称,请画出两个图形.
 见解析
【解析】试题分析:根据轴对称图形的定义和题目要求画出图形即可.
试题解析:【解析】
如图所示:
见解析
【解析】试题分析:根据轴对称图形的定义和题目要求画出图形即可.
试题解析:【解析】
如图所示: 某人沿倾斜角为β的斜坡前进100m,则他上升的最大高度是( )m
A.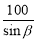 B.
B.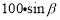 C.
C.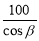 D.
D.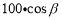
 B
【解析】
试题分析:设他上升的最大高度是hm,根据坡角及三角函数的定义即可求得结果.
设他上升的最大高度是hm,由题意得
,解得
故选B.
B
【解析】
试题分析:设他上升的最大高度是hm,根据坡角及三角函数的定义即可求得结果.
设他上升的最大高度是hm,由题意得
,解得
故选B. 下列属于分式方程的是( )
A. 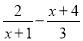 B.
B. 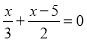
C. 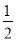 (x-1)=
(x-1)=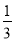 x D.
x D. 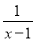 -x=1
-x=1
 D
【解析】试题解析:A,不是等式,所以不是方程,故不是分式方程.
B,C是一元一次方程,不是分式方程.
D.是分式方程.
故选D.
D
【解析】试题解析:A,不是等式,所以不是方程,故不是分式方程.
B,C是一元一次方程,不是分式方程.
D.是分式方程.
故选D. 如图,这是由一个边长为a的正方形沿一条对角线的方向平移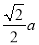 得到的图形,
得到的图形,
① 数一数这个图案中共有几个正方形;
② 若按此方法连续做4次平移,可得怎样的图案?该图案中共有几个正方形?

 3;15
【解析】试题分析:(1)根据正方形的定义即可得到答案.
(2)按此方法连续作4次平移画出图形,即可知道答案.
试题解析:
【解析】
(1)图中有3个正方形.
(2)图象如图所示,一共有15个正方形.
3;15
【解析】试题分析:(1)根据正方形的定义即可得到答案.
(2)按此方法连续作4次平移画出图形,即可知道答案.
试题解析:
【解析】
(1)图中有3个正方形.
(2)图象如图所示,一共有15个正方形.