��Ŀ����
�ڡ�ABC�У�OE��AB��OF��AC��OE=OF��
��1����ͼ������O��BC���е�ʱ����˵��AB=AC��
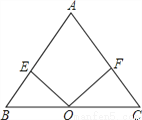
��2����ͼ������O�ڡ�ABC�ڲ�ʱ����OB=OC����˵��AB��AC�Ĺ�ϵ��
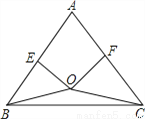
��3������O�ڡ�ABC�ⲿʱ����OB=OC�����ж�AB��AC�Ĺ�ϵ��������ͼ�Σ�д��������ɣ�����˵�����ɣ�
 ������
�������������������1��֤��BOE�ա�COF���ɵá�B=��C��ͨ���ȽǶԵȱߣ��ó�AB=AC��
��2���루1�����ƣ���֤�á�BOE�ա�COF�á�OBE=��OCF��OB=OC�����OBC=��OCB����֤�á�ABC=��ACB�����ݵȽǶԵȱߵó�AB=AC��
��3����ǰ���ʵĽ����̿�֪��BC�Ĵ�ֱƽ�������A�Ľ�ƽ�����غ�ʱ��AB=AC�Ľ��۲ų������������������ߺ�һ����...
������
�������������������1��֤��BOE�ա�COF���ɵá�B=��C��ͨ���ȽǶԵȱߣ��ó�AB=AC��
��2���루1�����ƣ���֤�á�BOE�ա�COF�á�OBE=��OCF��OB=OC�����OBC=��OCB����֤�á�ABC=��ACB�����ݵȽǶԵȱߵó�AB=AC��
��3����ǰ���ʵĽ����̿�֪��BC�Ĵ�ֱƽ�������A�Ľ�ƽ�����غ�ʱ��AB=AC�Ľ��۲ų������������������ߺ�һ����...
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�ij������б��Ϊ�µ�б��ǰ��100m���������������߶���( )m
A.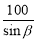 B.
B.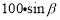 C.
C.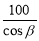 D.
D.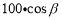
 B
��������
����������������������߶���hm�������½Ǽ����Ǻ����Ķ��弴����ý��.
�������������߶���hm���������
�����
��ѡB.
B
��������
����������������������߶���hm�������½Ǽ����Ǻ����Ķ��弴����ý��.
�������������߶���hm���������
�����
��ѡB. ���㣺20162��2016��2015.
 2016
����������������������ṫ��ʽ���ֽ���ʽ����ȷ������ʽ2016������ȡ����ʽ����.
���������20162��2016��2015
=2016����2016-2015��
=2016.
2016
����������������������ṫ��ʽ���ֽ���ʽ����ȷ������ʽ2016������ȡ����ʽ����.
���������20162��2016��2015
=2016����2016-2015��
=2016. ��ͼ��������һ���߳�Ϊa����������һ���Խ��ߵķ���ƽ��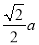 �õ���ͼ�Σ�
�õ���ͼ�Σ�
�� ��һ�����ͼ���й��м��������Σ�
�� �����˷���������4��ƽ�ƣ��ɵ�������ͼ������ͼ���й��м��������Σ�

 3��15
�������������������1�����������εĶ��弴�ɵõ��𰸣�
��2�����˷���������4��ƽ�ƻ���ͼ�Σ�����֪���𰸣�
���������
��������
��1��ͼ����3�������Σ�
��2��ͼ����ͼ��ʾ��һ����15�������Σ�
3��15
�������������������1�����������εĶ��弴�ɵõ��𰸣�
��2�����˷���������4��ƽ�ƻ���ͼ�Σ�����֪���𰸣�
���������
��������
��1��ͼ����3�������Σ�
��2��ͼ����ͼ��ʾ��һ����15�������Σ� ��ͼ��ʾ����ABC����ƽ�Ƶõ���DEF����֪CE��2 cm��AC��3 cm��AB��4 cm����A��90�㣬��CF��_________cm��ƽ�Ƶľ�����_________��
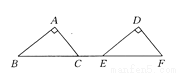
 7 7 cm
�������������������Rt��ABC�У��ɹ��ɶ����ã�
BC������5��cm����
�ߡ�ABC����ƽ�Ƶõ���DEF��
��EF��BC��5cm��
��CF��CE��EF��2��5��7��cm����
��C����F���Ӧ��
��ƽ�Ƶľ�����CF�ij��ȣ�
��ƽ�Ƶľ�����7cm��
�ʴ�Ϊ��7��7cm��
7 7 cm
�������������������Rt��ABC�У��ɹ��ɶ����ã�
BC������5��cm����
�ߡ�ABC����ƽ�Ƶõ���DEF��
��EF��BC��5cm��
��CF��CE��EF��2��5��7��cm����
��C����F���Ӧ��
��ƽ�Ƶľ�����CF�ij��ȣ�
��ƽ�Ƶľ�����7cm��
�ʴ�Ϊ��7��7cm�� �ڡ�ABC�У���AD��BE����H�㣬��BH=AC�����ABC=______��
 45���135��
����������������
��2�������
��1����ͼ��1����
�ߡ�BHD=��AHE���֡�AEH=��ADC=90�㣬���DAC+��C=90�㣬��HAE+��AHE=90�㣬
���AHE=��C�����C=��BHD��
��BH=AC����HBD=��DAC����C=��BHD�����HBD�ա�CAD����AD=BD��
���ABC=45�㣻
��2����ͼ��2�����ɣ�1���Ľ�...
45���135��
����������������
��2�������
��1����ͼ��1����
�ߡ�BHD=��AHE���֡�AEH=��ADC=90�㣬���DAC+��C=90�㣬��HAE+��AHE=90�㣬
���AHE=��C�����C=��BHD��
��BH=AC����HBD=��DAC����C=��BHD�����HBD�ա�CAD����AD=BD��
���ABC=45�㣻
��2����ͼ��2�����ɣ�1���Ľ�... ��ͼ���ڡ�ABC�У���C=60�㣬��B=50�㣬D��BC��һ�㣬DE��AB�ڵ�E��DF��AC�ڵ�F�����EDF�Ķ���Ϊ��������
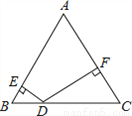
A. 90�� B. 100�� C. 110�� D. 120��
 C
����������������
�ڡ�ABC�У��ߡ�C=60�㣬��B=50�㣬���A=70�㣮
��DE��AB�ڵ�E��DF��AC�ڵ�F�����AED=��AFD=90�㣬���EDF=360�㩁��A����AED����AFD=110�㣮��ѡC��
C
����������������
�ڡ�ABC�У��ߡ�C=60�㣬��B=50�㣬���A=70�㣮
��DE��AB�ڵ�E��DF��AC�ڵ�F�����AED=��AFD=90�㣬���EDF=360�㩁��A����AED����AFD=110�㣮��ѡC�� ��ͼ���ı���ABCD�ĶԽ���AC��BD�ཻ��O�㣬��1=��2����3=��4��
��֤��(1)��ABC�ա�ADC��(2)BO=DO��
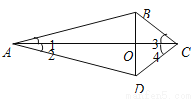
 (1)��֤�����̼�������(2)��֤�����̼�����
�����������������(1)�����ݡ�1=��2��AC=AC����3=��4�õ���ABC�͡�ADCȫ�ȣ�(2)������ȫ�ȵó�AB=AD��Ȼ���ϡ�1=��2��AO=AO�ó���ABO�͡�ADOȫ�ȣ��Ӷ��õ�BO=DO.
���������(1)���ڡ�ABC�͡�ADC�С��ABC�ա�ADC��
(2)���ߡ�ABC�ա�ADC ��AB=AD �ڡ�ABO�͡�ADO��...
(1)��֤�����̼�������(2)��֤�����̼�����
�����������������(1)�����ݡ�1=��2��AC=AC����3=��4�õ���ABC�͡�ADCȫ�ȣ�(2)������ȫ�ȵó�AB=AD��Ȼ���ϡ�1=��2��AO=AO�ó���ABO�͡�ADOȫ�ȣ��Ӷ��õ�BO=DO.
���������(1)���ڡ�ABC�͡�ADC�С��ABC�ա�ADC��
(2)���ߡ�ABC�ա�ADC ��AB=AD �ڡ�ABO�͡�ADO��... ����˵����ȷ���У�������
��4��x��3��1�Ľ⣻�ڲ���ʽx��2��0�Ľ�������������x��5�Dz���ʽx+2��3�Ľ⼯����x=3�Dz���ʽx+2��1�Ľ⣻�ݲ���ʽx+2��5���������������⣮
A��1�� B��2�� C��3�� D��4��
 B.
��������
�����������x��3��1�ã�x��4������4����x��3��1�Ľ⣬�ʢٴ�����ʽx��2��0�Ľ�������������˵����ȷ���ʢ���ȷ���ⲻ��ʽx+2��3�ã�x��1������x��5���Dz���ʽx+2��3�Ľ⼯���ʢ۴��ⲻ��ʽx+2��1�ã�x��-1,����x=3�Dz���ʽx+2��1�Ľ⣬�ʢ���ȷ���ⲻ��ʽx+2��5�ã�x��3,��������������Ϊ1��2��2��.�ʢݴ���.
��ѡB.
B.
��������
�����������x��3��1�ã�x��4������4����x��3��1�Ľ⣬�ʢٴ�����ʽx��2��0�Ľ�������������˵����ȷ���ʢ���ȷ���ⲻ��ʽx+2��3�ã�x��1������x��5���Dz���ʽx+2��3�Ľ⼯���ʢ۴��ⲻ��ʽx+2��1�ã�x��-1,����x=3�Dz���ʽx+2��1�Ľ⣬�ʢ���ȷ���ⲻ��ʽx+2��5�ã�x��3,��������������Ϊ1��2��2��.�ʢݴ���.
��ѡB. 
