题目内容
20.我们新定义一种三角形,若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为“奇高三角形”.如图1,在△ABC中,AD为BC边上的高,若AB2-AC2=AD2,则△ABC为奇高三角形.(1)求证:BD=AC;
(2)若在图1中∠BAC=90°,BC=a,AC=b,BA=c,
①求证:c2=ab;
②D是(选填“是”或“不是”)BC的黄金分割点;
(3)若图1中的奇高三角形,满足BA=BC,过D作DE∥AC交AB于E(如图2),试探究线段DE与DC的大小关系并证明.
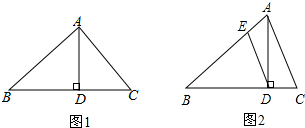
分析 (1)根据勾股定理得出AD2=AB2-BD2,即可得出答案;
(2)①根据已知得出c2-b2=AD2,证△BAD∽△ACD,推出AD2=BD×CD=b(a-b)=ab-b2,即可得出答案;②证△CAD∽△CBA,推出AC2=CD×BC,求出BD2=AC2=b2=CD×BC即可;
(3)过B作BM⊥DE于M,求出DE=2DM,证△ADC≌△BMD,推出DC=DM即可.
解答 (1)证明:∵AB2-AC2=AD2,
在Rt△ADB中,由勾股定理得:AD2=AB2-BD2,
∴AC2=BD2,
∴BD=AC;
(2)解:①∵∠BAC=90°,BC=a,AC=b,BA=c,△ABC为奇高三角形,
∴c2-b2=AD2,
∵AD⊥BC,
∴∠BAC=∠ADC=∠ADB=90°,
∴∠B+∠BAD=90°,∠BAD+∠CAD=90°,
∴∠B=∠CAD,
∴△BAD∽△ACD,
∴$\frac{AD}{BD}$=$\frac{CD}{AD}$,
∴AD2=BD×CD=b(a-b)=ab-b2,
∴c2-b2=ab-b2,
∴c2=ab;
②解:D是BC的黄金分割点,
理由是:∵∠C=∠C,∠CAD=∠B,
∴△CAD∽△CBA,
∴$\frac{AC}{CD}$=$\frac{BC}{AC}$,
∴AC2=CD×BC,
∵AC=BD=b,BC=a,
∴BD2=AC2=b2=CD×BC,
∴D是BC的黄金分割点,
故答案为:是;
(3)DE=2DC,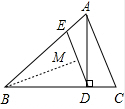
证明:过B作BM⊥DE于M,
∵AD⊥BC,
∴∠BMD=∠ADC=90°,
∵DE∥AC,
∴∠C=∠BDE,∠BAC=∠BED,
∵AB=BC,
∴∠BAC=∠C,
∴∠BED=∠BDE,
∴BE=BD,
∵BM⊥DE,
∴DM=ME,
即DE=2DM,
∵由(1)知:BD=AC,
在△ADC和△BMD中
$\left\{\begin{array}{l}{∠C=∠BDM}\\{∠ADC=∠BMD}\\{AC=BD}\end{array}\right.$
∴△ADC≌△BMD,
∴DC=DM,
∵DE=2DM,
∴DE=2DC.
点评 本题考查了等腰三角形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定,勾股定理的应用,能综合运用性质进行推理是解此题的关键,有一定的难度.

 学业测评一课一测系列答案
学业测评一课一测系列答案| A. | x<1 | B. | x≠1 | C. | x≥1 | D. | x≤1 |
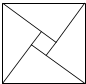 四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为1,大正方形面积为13,直角三角形的两条直角边为a、b,那么(a+b)2的值是25.
四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为1,大正方形面积为13,直角三角形的两条直角边为a、b,那么(a+b)2的值是25.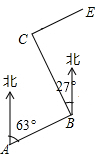 柳林乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东63°方向到B村,从B村沿北偏西27°方向到C村,水渠从C村沿北偏东63°方向修建,可以保持AB的方向一致.
柳林乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东63°方向到B村,从B村沿北偏西27°方向到C村,水渠从C村沿北偏东63°方向修建,可以保持AB的方向一致.
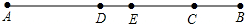 如图所示,线段AB=8cm,E为线段AB的中点,点C为线段EB上一点,且EC=3cm,点D为线段AC的中点,求线段DE的长度.
如图所示,线段AB=8cm,E为线段AB的中点,点C为线段EB上一点,且EC=3cm,点D为线段AC的中点,求线段DE的长度.