题目内容
在△ABC中,BC的垂直平分线与AB边所在的直线相交所得的锐角等于60°,则∠B的度数为 .
考点:线段垂直平分线的性质
专题:
分析:先化成图形,根据直角三角形两锐角互余求出即可.
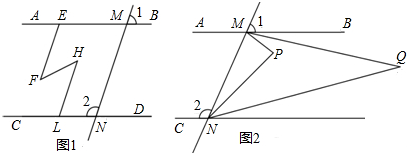
解答:解:分为两种情况:如图1,∵BC的垂直平分线与AB所在的直线相交所得到锐角为60°,
∴∠B=90°-60°=30°,
如图2,AB的垂直平分线与AC相交时,
∠DEB=60°,∠EMB=90°,
∴∠EBM=90°-60°=30°,
∴∠ABC=150°,
故答案为:30°或150°.

∴∠B=90°-60°=30°,
如图2,AB的垂直平分线与AC相交时,

∠DEB=60°,∠EMB=90°,
∴∠EBM=90°-60°=30°,
∴∠ABC=150°,
故答案为:30°或150°.
点评:本题考查了线段垂直平分线的性质,直角三角形两锐角互余的性质的应用,难点在于要分情况讨论,作出图形更形象直观.

练习册系列答案
相关题目
关于x的不等式组
的解集在数轴上表示为( )
|
A、 |
B、 |
C、 |
D、 |
 如图,已知AB=2,BG=3,GE=4.ED=5,△BCG和△EFG的面积和是24,△AGF和△CDG的面积和是51,则△ABC与△DEF的面积和是
如图,已知AB=2,BG=3,GE=4.ED=5,△BCG和△EFG的面积和是24,△AGF和△CDG的面积和是51,则△ABC与△DEF的面积和是 如图,将长方形纸片ABCD沿对角线BD折叠,使点C落在点C′处,BC′交AD于点E.若∠BDC=55°,求∠ADC′的度数.
如图,将长方形纸片ABCD沿对角线BD折叠,使点C落在点C′处,BC′交AD于点E.若∠BDC=55°,求∠ADC′的度数.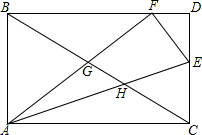 如图,矩形ABDC中,AB、AC长分别为6和10,点E在边CD上,将△ACE沿线段AE翻折,得到△AEF,点C落在BD边上,AF、AE分别交对角线BC于点G、H,则GH的长为
如图,矩形ABDC中,AB、AC长分别为6和10,点E在边CD上,将△ACE沿线段AE翻折,得到△AEF,点C落在BD边上,AF、AE分别交对角线BC于点G、H,则GH的长为