题目内容
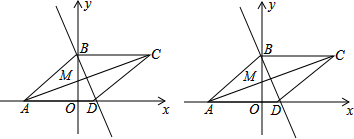
如图,菱形ABCD在平面直角坐标系中,AD在x轴上,直线AB的解析式为y=
x+3,连接AM交y轴于M.
(1)求点D的坐标;
(2)动点P从点A出发以每秒1个单位长度的速度沿射线AD方向运动,过P作PQ⊥BD于Q.设运动的时间为t秒,PQ的长度为y,求y与t之间的函数关系式,并直接写出t的取值范围;
(3)在(2)的条件下,是否存在t的值使以P、Q、M、A为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.
| 3 |
| 4 |
(1)求点D的坐标;
(2)动点P从点A出发以每秒1个单位长度的速度沿射线AD方向运动,过P作PQ⊥BD于Q.设运动的时间为t秒,PQ的长度为y,求y与t之间的函数关系式,并直接写出t的取值范围;
(3)在(2)的条件下,是否存在t的值使以P、Q、M、A为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.

考点:一次函数综合题
专题:
分析:(1)菱形是邻边相等的平行四边形,求点D的坐标,已知点A、B的坐标(由解析式可得),可以先利用勾股定理求出AB的长度,然后再又AB=AD求得点D的坐标.
(2)记AC、BD相交于点N,则若表示PQ的长,我们可以利用△AND∽△PQD,得到一个比例关系,进而可以由与t相关的PD表示PQ,从而确定y与t的函数关系式.注意P延AD方向运动,可能在D的左边,也可能在D上,或在右边,需要分开讨论.
(3)已知AM∥PQ,现只需得到AM=PQ,即可得到四边形AMQP为平行四边形,所以先求出AC直线方程确定M点坐标,然后根据(2)的结论就可以得到关于t的方程,进而求得t.
(2)记AC、BD相交于点N,则若表示PQ的长,我们可以利用△AND∽△PQD,得到一个比例关系,进而可以由与t相关的PD表示PQ,从而确定y与t的函数关系式.注意P延AD方向运动,可能在D的左边,也可能在D上,或在右边,需要分开讨论.
(3)已知AM∥PQ,现只需得到AM=PQ,即可得到四边形AMQP为平行四边形,所以先求出AC直线方程确定M点坐标,然后根据(2)的结论就可以得到关于t的方程,进而求得t.
解答:解:(1)由直线y=
x+3交x轴、y轴分别于A、B两点,所以A点坐标为(-4,0),B点坐标为(0,3)
在Rt△AOB中,
∵AO=4,BO=3
∴AB=5
在菱形ABCD中
∵AB=BC=CD=AD=5,BC∥AD
∴C点坐标为(5,3),D点坐标为(-1,0)
(2)如图,
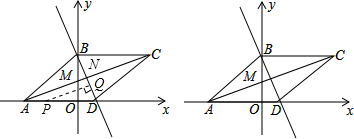
记菱形对角线AC、BD相交于点,根据题意在AD上任找一点P,过点P作PQ⊥ND于Q,则∠AND=90°.
∵∠PQD=∠AND=90°
∴PQ∥AN
∴
=
在Rt△BOD中,
∵BO=3,OD=1
∴BD=
∴ND=
BD=
在Rt△AND中,
∵AD=5,ND=
∴AN=
∵AP=t
∴PD=5-t
∴
=
∴PD=-
t+
即y=-
t+
(0≤t<5)
如图,
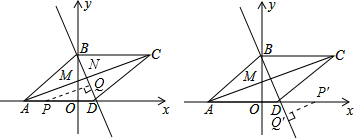
在AD的延长线上任找一点P′,过P′作P′Q′⊥BD于Q′
同理有
=
,AP′=t
∵P′D=AP′-AD=t-5
∴P′Q′=
t-
即y=
t-
(t>5)
则y与t之间的函数关系为y=
(3)∵PQ∥AM
∴若有PQ=AM,则由PQAM为顶点的四边形就为平行四边形
设直线AC的解析式为y=kx+b,将A(-4,0),C(5,3)代入整理得,直线AC的解析式为y=
x+
∵M在直线AC上
∴M的坐标为(0,
)
在Rt△AOM中
∵AO=4,MO=
∴AM=
当0≤t<5时,
=-
t+
,解得t=
当t>5时,
=
t-
,解得t=
(如图,应有此两种情况,本题不需要辅助线,此图仅辅助理解)

故当
s和
s时,A、M、P、Q四点为顶点组成的四边形为平行四边形.
| 3 |
| 4 |
在Rt△AOB中,
∵AO=4,BO=3
∴AB=5
在菱形ABCD中
∵AB=BC=CD=AD=5,BC∥AD
∴C点坐标为(5,3),D点坐标为(-1,0)
(2)如图,

记菱形对角线AC、BD相交于点,根据题意在AD上任找一点P,过点P作PQ⊥ND于Q,则∠AND=90°.
∵∠PQD=∠AND=90°
∴PQ∥AN
∴
| PD |
| PQ |
| AD |
| AN |
在Rt△BOD中,
∵BO=3,OD=1
∴BD=
| 10 |
∴ND=
| 1 |
| 2 |
| ||
| 2 |
在Rt△AND中,
∵AD=5,ND=
| ||
| 2 |
∴AN=
3
| ||
| 2 |
∵AP=t
∴PD=5-t
∴
| 5-t |
| PQ |
| 5 | ||||
|
∴PD=-
3
| ||
| 10 |
3
| ||
| 2 |
即y=-
3
| ||
| 10 |
3
| ||
| 2 |
如图,

在AD的延长线上任找一点P′,过P′作P′Q′⊥BD于Q′
同理有
| P′D |
| P′Q′ |
| AD |
| AN |
∵P′D=AP′-AD=t-5
∴P′Q′=
3
| ||
| 10 |
3
| ||
| 2 |
即y=
3
| ||
| 10 |
3
| ||
| 2 |
则y与t之间的函数关系为y=
|
(3)∵PQ∥AM
∴若有PQ=AM,则由PQAM为顶点的四边形就为平行四边形
设直线AC的解析式为y=kx+b,将A(-4,0),C(5,3)代入整理得,直线AC的解析式为y=
| 1 |
| 3 |
| 4 |
| 3 |
∵M在直线AC上
∴M的坐标为(0,
| 4 |
| 3 |
在Rt△AOM中
∵AO=4,MO=
| 4 |
| 3 |
∴AM=
4
| ||
| 3 |
当0≤t<5时,
4
| ||
| 3 |
3
| ||
| 10 |
3
| ||
| 2 |
| 5 |
| 9 |
当t>5时,
4
| ||
| 3 |
3
| ||
| 10 |
3
| ||
| 2 |
| 85 |
| 9 |
(如图,应有此两种情况,本题不需要辅助线,此图仅辅助理解)

故当
| 5 |
| 9 |
| 85 |
| 9 |
点评:此题难度较大,综合运用知识较多.菱形的性质是求解第一问的关键,要充分利用其为邻边相等的平行四边形这个定义.第二问的整体难度不算太高,但是想得高分很难,因为我们常常忽略P点运动到D点右边的情形,所以对于动点问题养成紧抓题干字眼,考虑遍所有情形等习惯才能让我们的试卷锦上添花.第三问其实向我们传递着一个做综合题的技巧,这一问的思路往往是紧扣上一问的结论的.我们由第二问得到了PQ长度的关系,那么仅仅利用函数的思想就可以轻松的解决第三问结论,如果另当新题,恐怕思路难以找寻.

练习册系列答案
相关题目
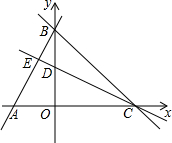 如图,在坐标平面中,直线y=2x+12分别交x轴、y轴于A、B,把△AOB绕点O旋转,使点B落在x轴正半轴点C处,A落在y轴上点D处,直线CD于AB相交于点E.
如图,在坐标平面中,直线y=2x+12分别交x轴、y轴于A、B,把△AOB绕点O旋转,使点B落在x轴正半轴点C处,A落在y轴上点D处,直线CD于AB相交于点E.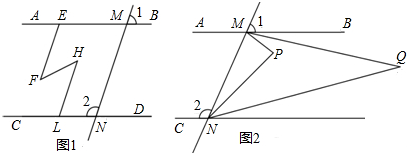
 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,求出抛物线y=ax2的解析式.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,求出抛物线y=ax2的解析式. 如图,BD,CE,AF分别是△ABC的角平分线,且相交于点O,OH⊥BC于H,试问∠1=∠2?请说明理由.
如图,BD,CE,AF分别是△ABC的角平分线,且相交于点O,OH⊥BC于H,试问∠1=∠2?请说明理由.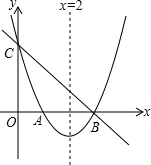 如图,直线y=-x+3与x轴,y轴分别相交于点B,点C,经过B、C两点的抛物线y=ax2+bx+c(a≠0)与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
如图,直线y=-x+3与x轴,y轴分别相交于点B,点C,经过B、C两点的抛物线y=ax2+bx+c(a≠0)与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.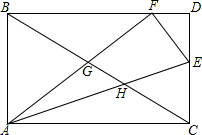 如图,矩形ABDC中,AB、AC长分别为6和10,点E在边CD上,将△ACE沿线段AE翻折,得到△AEF,点C落在BD边上,AF、AE分别交对角线BC于点G、H,则GH的长为
如图,矩形ABDC中,AB、AC长分别为6和10,点E在边CD上,将△ACE沿线段AE翻折,得到△AEF,点C落在BD边上,AF、AE分别交对角线BC于点G、H,则GH的长为