��Ŀ����
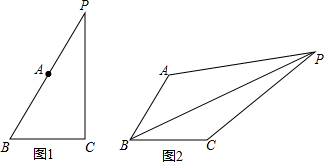
18����ѧ����ϣ���ʦ�������һ�����⣺���AB=BC����ABC=60�㣬��APC=30�㣬����PB����ôPA��PB��PC֮����������ĵ�����ϵ�أ�����˼������ͬѧ���������µĽ�����С�٣��ҽ�ͼ�ν��������⻯���õ�P��BA�ӳ����ϣ���ͼ1�����õ���һ�����룺PA2+PC2=PB2��
С�����Ҽ����P�ڡ�ABC���ڲ���������Ŀ���������ͼ�ξ��С����˵���߶Ρ����ص㣬����������ת������⣬��ת��PAB��õ���P��CB�����ҿ��Ƴ���PBP�䣬��PCP��ֱ��ǵȱ������Ρ�ֱ�������Σ����ܵõ������֤��������
��ʱ��ʦ��ͬѧ��˵����������������⣺
��1����ͼ2����P�ڡ�ABC���ڲ���
��PA=4��PC=$2\sqrt{3}$��PB=2$\sqrt{7}$��
���õ�ʽ��ʾPA��PB��PC֮���������ϵ����֤����
��2�����ڵ�P������λ�ã��Ƿ�ʼ�վ��Т��еĽ��ۣ����ǣ���֤���������ǣ������˵����
���� ��1�����ݽ��۴��뼴����д��
��2�����ݡ�ABP�ա�CBP��ó�PA=P��C����A=��BCP�䣬���ɵó�PA��PB��PC֮���������ϵ��
��3������P��CB���ӳ�����ʱ���ó�PA2+PB2=PC2��
��� �⣺��1����PB=$\sqrt{P{A}^{2}+P{C}^{2}}=\sqrt{{4}^{2}+��2\sqrt{3}��^{2}}$=$2\sqrt{7}$��
�ʴ�Ϊ��$2\sqrt{7}$��
��PA2+PC2=PB2��
֤��������PBP��=��ABC=60�㣬��ʹBP��=BP������P��C��P��P����ͼ1��
�ߡ�ABC=PBP��
���ABP=��CBP�䣬
��AB=CB��
�ڡ�ABP���CBP���У�
$\left\{\begin{array}{l}{AB=BC}\\{��ABP=��CBP'}\\{BP=BP'}\end{array}\right.$��
���ABP�ա�CBP�䣬
��PA=P��C����A=��BCP�䣬
���ı���ABCP�У�
�ߡ�ABC=60�㣬��APC=30�㣬
���A+��BCP=270�㣬
���BCP��+��BCP=270�㣬
���PCP��=360��-����BCP��+��BCP��=90�㣬
�ߡ�PBP���ǵȱ������Σ�
��PP��=PB��
��Rt��PCP����P'C2+PC2=P'P2��
��PA2+PC2=PB2��
��2����P������λ��ʱ������ʼ�վ��Т��в���Ľ��ۣ�������
��ͼ2������P��CB���ӳ�����ʱ��
����ΪPA2+PB2=PC2��
���� ���⿼���˼��α任���⣬����Ĺؼ�����������ȫ�������ε��ж������Լ�������ȫ�ȵ����ʣ�

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д� ��ͼ��һ����5����С��ͬ���ⳤΪ1���������ɵļ����壬���й�������������˵����ȷ���ǣ�������
��ͼ��һ����5����С��ͬ���ⳤΪ1���������ɵļ����壬���й�������������˵����ȷ���ǣ�������| A�� | ����ͼ�����Ϊ5 | B�� | ����ͼ�����Ϊ3 | C�� | ����ͼ�����Ϊ5 | D�� | ����ͼ�����Ϊ3 |
| ����ʱ��x�� | 4 | 10 | 36 |
| �г���yԪ | 90 | 51 | 90 |
��y=ax+b��a��0���� ��y=a��x-h��2+k�� a��0���� ��y=$\frac{a}{x}$��a��0����
���ѡ��ĺ���������Ǣڣ�
��2��������ѡȡ�ĺ�������ü�������ж�����ʱ�г�����ͣ���ͼ۸��Ƕ��٣�
| A�� | �� | B�� | ��Ψһһ���� | C�� | ����������� | D�� | ����ȷ�� |
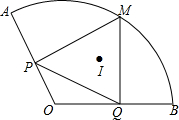 ��ͼ������AOB�İ뾶Ϊ2����AOB=120�㣬��P��Q�ǰ뾶OA��OB�ϵĶ��㣬M��$\widehat{AB}$��һ�㣬��MP��OA��P��MQ��OB��Q��I�ǡ�MPQ�����ģ���MI�ij��ȵķ�Χ�ǣ�������
��ͼ������AOB�İ뾶Ϊ2����AOB=120�㣬��P��Q�ǰ뾶OA��OB�ϵĶ��㣬M��$\widehat{AB}$��һ�㣬��MP��OA��P��MQ��OB��Q��I�ǡ�MPQ�����ģ���MI�ij��ȵķ�Χ�ǣ�������| A�� | 1��MI��$\sqrt{3}$ | B�� | $\frac{\sqrt{3}}{2}$��MI��1 | C�� | $\frac{1}{2}$��MI��$\frac{\sqrt{3}}{2}$ | D�� | $\sqrt{3}$-1��MI��1 |
 ��4����ȫ��ͬ��С���������������ͼ��ʾ������ͼ�Σ���ô��������ͼ�ǣ�������
��4����ȫ��ͬ��С���������������ͼ��ʾ������ͼ�Σ���ô��������ͼ�ǣ�������


