题目内容
13.直角坐标系中点A坐标为(5,3),B坐标为(1,0),将点A绕点B逆时针旋转90°得到点C,则点C的坐标为(-2,4).分析 根据题意画出图形,易证△ADB≌△BEC,求出CE、OE的长即可求出C的坐标.
解答 解:如图所示,点A绕点B逆时针旋转90°到点C,
∵A坐标为(5,3),B坐标为(1,0),
∴AD=3,BD=4,
∴AB=5,
根据旋转的性质,AB=BC,
∵∠ABC=90°,
∴∠EBC+∠ABD=90°,
∵∠DAB+∠ABD=90°,
∴∠EBC=∠DAB.
在△EBC和△BAD中
$\left\{\begin{array}{l}{∠CEB=∠BDA=90°}\\{∠EBC=∠DAB}\\{AB=BC}\end{array}\right.$,
∴△EBC≌△BAD,
∴CE=BD=4,BE=AD=3,
∵OB=1,
∴OE=2,
∴C(-2,4).
故答案为:(-2,4).
点评 本题主要考查了旋转变换和三角形全等的判定与性质,证明△EBC≌△BAD是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
8.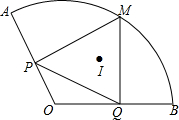 如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )
如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )
 如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )
如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )| A. | 1≤MI≤$\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$≤MI≤1 | C. | $\frac{1}{2}$≤MI≤$\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$-1≤MI≤1 |
18.芝麻作为食品和药物,均广泛使用,经测算,一粒芝麻重量约有0.00000201kg,用科学记数法表示10粒芝麻的重量为( )
| A. | 2.01×10-6kg | B. | 2.01×10-5kg | C. | 20.1×10-7kg | D. | 20.1×10-6kg |
5.据国家统计局核算,2014年全年国内生产总值(GDP)超过63个亿,比2013年增长7.4%,数据“63万亿”用科学记数法表示为( )
| A. | 63×104 | B. | 6.3×105 | C. | 6.3×1012 | D. | 6.3×1013 |
 用4个完全相同的小正方体组成如左下图所示的立体图形,那么它的主视图是( )
用4个完全相同的小正方体组成如左下图所示的立体图形,那么它的主视图是( )


