题目内容
18.已知关于x的一元二次方程kx2-2(k-1)x+k-2=0(k≠0)(1)小明考查后说,它总有两个不相等的实数根.
(2)小华补充说,其中一个根与k无关.
请你说说其中的道理.
分析 (1)首先判断出△=4(k-1)2-4k(k-2)=4>0,即可判定方程有两个不相等的实数根;
(2)当x=1时,方程左右两边均为0,方程的根与k无关.
解答 解:(1)∵△=4(k-1)2-4k(k-2)=4>0,
∴一元二次方程kx2-2(k-1)x+k-2=0(k≠0)总有两个不相等的实数根;
(2)当x=1时,k-2(k-1)+k-2=0,
即一元二次方程kx2-2(k-1)x+k-2=0(k≠0)有一根为1,
x=1是一元二次方程kx2-2(k-1)x+k-2=0(k≠0)的根,与k无关.
点评 本题考查了根的判别式以及一元二次方程的解的知识,解答本题要掌握一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根,此题难度不大.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
8.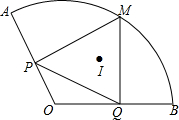 如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )
如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )
 如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )
如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )| A. | 1≤MI≤$\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$≤MI≤1 | C. | $\frac{1}{2}$≤MI≤$\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$-1≤MI≤1 |
9.下列命题中,真命题是( )
| A. | 等边三角形既是轴对称图形又是中心对称图形 | |
| B. | 两条对角线互相垂直且平分的四边形是正方形 | |
| C. | 有一个角是60°的等腰三角形是等边三角形 | |
| D. | 有两条对角线相等的四边形是矩形 |
6.把x2-4x+4分解因式,结果正确的是( )
| A. | (x-2)2 | B. | (x+2)2 | C. | (x-4)2 | D. | (x+4)2 |
13.掷一枚质地均匀的硬币10次,下列说法正确的是( )
| A. | 有5次正面朝上 | B. | 不可能10次正面朝上 | ||
| C. | 不可能10次正面朝下 | D. | 可能有5次正面朝上 |
10.已知∠A=25°,则∠A的补角等于( )
| A. | 65° | B. | 75° | C. | 155° | D. | 165° |
8.若正比例函数y=kx(k≠0)的图象经过点P(-2,3),则该函数的图象经过的点是( )
| A. | (3,-2) | B. | (1,-6) | C. | (2,-3) | D. | (-1,-6) |