题目内容
3.已知,一个样本有40个数据,58,61,60,59,59;58,58,57,57,57;57,56,56,56,56;56,56,51,56,55;55,55,55,54,54;,54,54,53,53,52;52,52,52,52,51;48,49,50,50,51;列出频数分布表并绘制样本频数分布直方图.
(1)计算最大值与最小值的差:13.
(2)取组距为2,则组数为7,应分为7组.
(3)列出频数分数表.
分析 (1)找出这组数据中的最大值和最小值,进行相减即可;
(2)用最大值和最小值的差除以组距,进而得到组距;
(3)列表统计各段内的频数,即可得出频数分布表.进而绘制出样本频数分布直方图.
解答 解:(1)最大值与最小值的差=61-48=13;
(2)取组距为2,则组数为13÷2=6.5≈7,应分为7组;
(3)频数分布表如下:
频数分布直方图如下:
故答案为13;7,7.
点评 本题考查了频率分布直方图,列频率分布表、画频率分布直方图的步骤:
(1)计算极差,即计算最大值与最小值的差;
(2)决定组距与组数(组数与样本容量有关,一般来说样本容量越大,分组就越多,样本容量不超过100时,按数据的多少,常分成5~12组);
(3)将数据分组;
(4)列频率分布表;
(5)画频率分布直方图.

练习册系列答案
相关题目
13. 如图,一个由5个大小相同、棱长为1的正方体搭成的几何体,下列关于这个几何体的说法正确的是( )
如图,一个由5个大小相同、棱长为1的正方体搭成的几何体,下列关于这个几何体的说法正确的是( )
 如图,一个由5个大小相同、棱长为1的正方体搭成的几何体,下列关于这个几何体的说法正确的是( )
如图,一个由5个大小相同、棱长为1的正方体搭成的几何体,下列关于这个几何体的说法正确的是( )| A. | 主视图的面积为5 | B. | 左视图的面积为3 | C. | 俯视图的面积为5 | D. | 俯视图的面积为3 |
14.某中学矩形了一次演讲比赛,分段统计参赛同学的成绩,结果如表所示(分数为整数,满分为100分):
则这次演讲比赛的同学的平均数为77分~86分.
| 分数段(分) | 61~70 | 71~80 | 81~90 | 91~100 |
| 人数(人) | 2 | 8 | 6 | 4 |
8.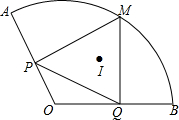 如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )
如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )
 如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )
如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )| A. | 1≤MI≤$\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$≤MI≤1 | C. | $\frac{1}{2}$≤MI≤$\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$-1≤MI≤1 |
15. 如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )
如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )
 如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )
如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )| A. | CD+DF=4 | B. | CD-DF=2$\sqrt{3}$-3 | C. | BC+AB=2$\sqrt{3}$+4 | D. | BC-AB=2 |
12.在不等式组$\left\{\begin{array}{l}{-x-1≤0}\\{\frac{3x-2}{2}≤x+1}\end{array}\right.$的解集中正整数的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
13.掷一枚质地均匀的硬币10次,下列说法正确的是( )
| A. | 有5次正面朝上 | B. | 不可能10次正面朝上 | ||
| C. | 不可能10次正面朝下 | D. | 可能有5次正面朝上 |
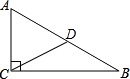 如图所示,在△ABC中,∠ACB=90°,BC=5cm,AC=10cm,CD为中线,以点C为圆心,以$\frac{5}{2}$$\sqrt{5}$cm为半径作圆,则点A,B,D与⊙C的位置关系如何.
如图所示,在△ABC中,∠ACB=90°,BC=5cm,AC=10cm,CD为中线,以点C为圆心,以$\frac{5}{2}$$\sqrt{5}$cm为半径作圆,则点A,B,D与⊙C的位置关系如何.