题目内容
某学校计划在总费用不超过2300元的限额内，租用汽车送234名学生和6名教师集体外出活动，每辆汽车上至少要一名教师．现有甲、乙两种大客车，它们的载客量和租金如下表：
（1）若设租甲种客车x（辆）、学校租车所需的总费用y（元），根据题意写出y与x之间的函数关系式 ．
（2）根据题意，求出（1）中函数的自变量x的取值；
（3）租车方案是怎样时，租车所需的总费用最少？最少的租车费用是多少？
| 甲种客车 | 乙种客车 | |
| 载客量（人/辆） | 45 | 30 |
| 租金（元/辆） | 400 | 280 |
（2）根据题意，求出（1）中函数的自变量x的取值；
（3）租车方案是怎样时，租车所需的总费用最少？最少的租车费用是多少？
考点：一次函数的应用
专题：
分析：（1）根据题意可列出y与x的等式关系，再化简整理得出x，y的表达式；
（2）根据45x+30（6-x）≥234和400x+280（6-x）≤2300组成不等式组，得出x的取值范围，进而求出租车方案；
（2）利用函数解析式，根据函数的性质，结合x的取值范围，求得y有最小值即可．
（2）根据45x+30（6-x）≥234和400x+280（6-x）≤2300组成不等式组，得出x的取值范围，进而求出租车方案；
（2）利用函数解析式，根据函数的性质，结合x的取值范围，求得y有最小值即可．
解答：解：（1）设租甲种客车x（辆）、学校租车所需的总费用y（元），依题意，
得y=500x+400（6-x）
整理，得y=100x+2400．
所以y与x的函数关系式为：y=100x+2400；
（2）依题意，得
解得4≤x≤
．
又∵x应为整数，
∴4≤x≤5．
（3）在y=100x+2400中，
∵k=100＞0，
∴y随x的增大而增大．
∴当x取最小值，即x=4时，y有最小值，最小值为y=100×4+2400=2600．
所以最节省费用的租车方案是：租用4辆甲种客车，2辆乙种客车．最节省费用为2800元．
得y=500x+400（6-x）
整理，得y=100x+2400．
所以y与x的函数关系式为：y=100x+2400；
（2）依题意，得
|
解得4≤x≤
| 31 |
| 6 |
又∵x应为整数，
∴4≤x≤5．
（3）在y=100x+2400中，
∵k=100＞0，
∴y随x的增大而增大．
∴当x取最小值，即x=4时，y有最小值，最小值为y=100×4+2400=2600．
所以最节省费用的租车方案是：租用4辆甲种客车，2辆乙种客车．最节省费用为2800元．
点评：此题主要考查了一次函数与一次不等式组的综合应用，由题意得出租用x辆甲种客车与总租金用y的函数关系是解决问题的关键．
练习册系列答案
相关题目
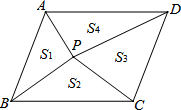如图，点P是?ABCD内的任意一点，连接PA、PB、PC、PD，得到△PAB、△PBC、△PCD、△PDA，设它们的面积分别是S1、S2、S3、S4，给出如下结论：
