题目内容
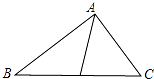
阅读理解如图，在△ABC中，AD平分∠BAC，求证：
| AB |
| BD |
| AC |
| CD |
小明在证明此题时，想通过证明三角形相似来解决，但发现图中无相似三角形，于是过点B作BE∥AC交AD的延长线于点E，构造△ACD∽△EBD，则
| AB |
| BD |
| AC |
| CD |
于是小明得出结论：在△ABC中，AD平分∠BAC，则
| AB |
| BD |
| AC |
| CD |
请完成小明的证明过程．
考点：相似三角形的判定与性质
专题：
分析：先过点B作BE∥AC交AD延长线于点E，由于BE∥AC，利用平行线分线段成比例定理的推论、平行线的性质，可得△BDE∽△CDA，∠E=∠DAC，再利用相似三角形的性质可有
=
，而利用AD时角平分线又知∠E=∠DAC=∠BAD，于是BE=AB，等量代换即可证．
| BD |
| DC |
| BE |
| AC |
解答：解：过点B作BE∥AC交AD延长线于点E，
∵BE∥AC，
∴∠DBE=∠C，∠E=∠CAD，
∴△BDE∽△CDA，
∴
=
，
又∵AD是角平分线，
∴∠E=∠DAC=∠BAD，
∴BE=AB，
∴
=
．
∵BE∥AC，
∴∠DBE=∠C，∠E=∠CAD，
∴△BDE∽△CDA，
∴
| BD |
| DC |
| BE |
| AC |
又∵AD是角平分线，
∴∠E=∠DAC=∠BAD，
∴BE=AB，
∴
| AB |
| BD |
| AC |
| CD |
点评：本题考查了角平分线的定义、相似三角形的判定和性质、平行线分线段成比例定理的推论．关键是作平行线．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
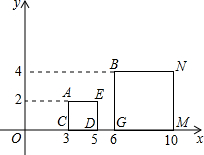如图，在直角坐标系中，点A、B的坐标分别为（3，2）、（6，4），AC⊥x轴于点C，BG⊥x轴于点G，分别以AC、BG为边作正方形ACDE和正方形BGMN；
某服装公司试销一种成本为每件50元的T恤衫，规定试销时的销售单价不低于成本价，又不高于每件70元，试销中销售量y（件）与销售单价x（元）的关系可以近似的看作一次函数（如图）．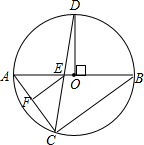
在⊙O中，已知AB为直径，C、D是⊙O上两点，且C、D在AB的两侧，OD⊥AB，CD交AB于E点，过E作EF∥BC交AC于F点．
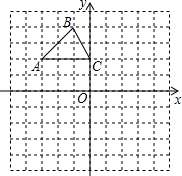如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别是A（-3，2），