题目内容
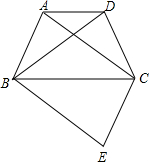 如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.(1)求证:四边形ABEC是平行四边形.
(2)若AD=CD=6,∠ADC=120°,求四边形ABEC的面积.
考点:翻折变换(折叠问题),平行四边形的判定与性质,等腰梯形的性质
专题:
分析:(1)由四边形ABCD为等腰梯形,AD∥BC,可得AB=DC,AC=BD,又由在平面内将△DBC沿BC翻折得到△EBC,可得EC=DC,DB=BE,继而可得:EC=AB,BE=AC,则可证得四边形ABEC是平行四边形;
(2)利用等腰梯形的性质,求得高和BC的长即可求得四边形ABEC的面积=2△ABC的面积.
(2)利用等腰梯形的性质,求得高和BC的长即可求得四边形ABEC的面积=2△ABC的面积.
解答:(1)证明:∵四边形ABCD为等腰梯形,AD∥BC,
∴AB=DC,AC=BD,
由折叠的性质可得:EC=DC,DB=BE,
∴EC=AB,BE=AC,
∴四边形ABEC是平行四边形.
(2)解:如图,
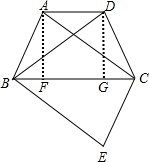
过点A、D分别作AF⊥BC,DG⊥BC,垂足分别为F、G,
∵AD∥BC,∠ADC=120°,
∴FG=AD=6,AF=DG,∠ABF=60°,
∵四边形ABCD为等腰梯形,
∴AB=DC=6,
∴BF=
AB=3,AF=
AB=3
,
在Rt△ABF和Rt△CDG中,
,
∴Rt△ABF≌Rt△CDG(HL),
∴BF=GC=3,
∴BC=12,
∴S四边形ABEC=2S△ABC=2×
×12×3
=36
.
∴AB=DC,AC=BD,
由折叠的性质可得:EC=DC,DB=BE,
∴EC=AB,BE=AC,
∴四边形ABEC是平行四边形.
(2)解:如图,

过点A、D分别作AF⊥BC,DG⊥BC,垂足分别为F、G,
∵AD∥BC,∠ADC=120°,
∴FG=AD=6,AF=DG,∠ABF=60°,
∵四边形ABCD为等腰梯形,
∴AB=DC=6,
∴BF=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
在Rt△ABF和Rt△CDG中,
|
∴Rt△ABF≌Rt△CDG(HL),
∴BF=GC=3,
∴BC=12,
∴S四边形ABEC=2S△ABC=2×
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题考查了等腰梯形的性质、折叠的性质以及平行四边形的性质.注意掌握数形结合思想的应用.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
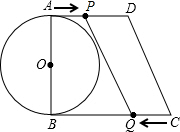 如图,AB是圆O的直径,AD、BC都垂直于AB,AD=13cm,BC=16cm,DC=5cm,点P、Q是动点,点P以1cm/s的速度由A向D运动,同时Q从C向B以2cm/s的速度运动,当其中一点到达时,另一点同时停止运动.
如图,AB是圆O的直径,AD、BC都垂直于AB,AD=13cm,BC=16cm,DC=5cm,点P、Q是动点,点P以1cm/s的速度由A向D运动,同时Q从C向B以2cm/s的速度运动,当其中一点到达时,另一点同时停止运动.
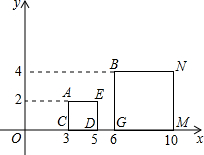 如图,在直角坐标系中,点A、B的坐标分别为(3,2)、(6,4),AC⊥x轴于点C,BG⊥x轴于点G,分别以AC、BG为边作正方形ACDE和正方形BGMN;
如图,在直角坐标系中,点A、B的坐标分别为(3,2)、(6,4),AC⊥x轴于点C,BG⊥x轴于点G,分别以AC、BG为边作正方形ACDE和正方形BGMN;
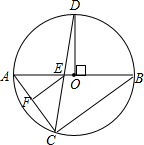 在⊙O中,已知AB为直径,C、D是⊙O上两点,且C、D在AB的两侧,OD⊥AB,CD交AB于E点,过E作EF∥BC交AC于F点.
在⊙O中,已知AB为直径,C、D是⊙O上两点,且C、D在AB的两侧,OD⊥AB,CD交AB于E点,过E作EF∥BC交AC于F点.