��Ŀ����
1��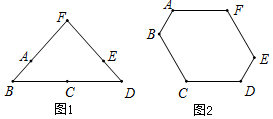 ��6���ֹ���β˳�ν½Ӷ��������θּ�ABCDEF���������ֹܿ���ת������֪���ֹܵij���ΪAB=DE=1�ף�BC=CD=EF=FA=2�ף����½ӵ㳤�Ⱥ��Բ��ƣ�
��6���ֹ���β˳�ν½Ӷ��������θּ�ABCDEF���������ֹܿ���ת������֪���ֹܵij���ΪAB=DE=1�ף�BC=CD=EF=FA=2�ף����½ӵ㳤�Ⱥ��Բ��ƣ���1��ת���ֹܵõ������θּܣ���ͼ1�����A��E֮��ľ�����$\frac{8}{3}$�ף�
��2��ת���ֹܵõ���ͼ2��ʾ�������θּܣ��С�A=��B=��C=��D=120�㣬���������������Ӷ���ʹ�øּܲ��ܻ�����������������ܳ��ȵ���Сֵ��3$\sqrt{7}$�ף�
���� ��1��ֻҪ֤��AE��BD����$\frac{AE}{DB}$=$\frac{AF}{FB}$���г����̼��ɽ�����⣮
��2���ֱ���������εĶԽ��߲��ұȽϴ�С�����ɽ�����⣮
��� �⣺��1����ͼ1�У���FB=DF��FA=FE��
���FAE=��FEA����B=��D��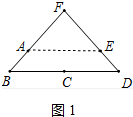
���FAE=��B��
��AE��BD��
��$\frac{AE}{DB}$=$\frac{AF}{FB}$��
��$\frac{AE}{4}$=$\frac{2}{3}$��
��AE=$\frac{8}{3}$��
�ʴ�Ϊ$\frac{8}{3}$��
��2����ͼ�У���BN��FA��N���ӳ�AB��DC���ڵ�M������BD��AD��BF��CF��
��RT��BFN�У��ߡ�BNF=90�㣬BN=$\frac{\sqrt{3}}{2}$��FN=AN+AF=$\frac{1}{2}$+2=$\frac{5}{2}$��
��BF=$\sqrt{B{N}^{2}+N{F}^{2}}$=$\sqrt{7}$��ͬ���õ�AC=DF=$\sqrt{7}$��
�ߡ�ABC=��BCD=120�㣬
���MBC=��MCB=60�㣬
���M=60�㣬
��CM=BC=BM��
�ߡ�M+��MAF=180�㣬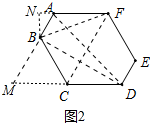
��AF��DM����AF=CM��
���ı���AMCF��ƽ���ı��Σ�
��CF=AM=3��
�ߡ�BCM=��CBD+��CDB=60�㣬��CBD=��CDB��
���CBD=��CDB=30�㣬�ߡ�M=60�㣬
���MBD=90�㣬
��BD=$\sqrt{D{M}^{2}-B{M}^{2}}$=2$\sqrt{3}$��ͬ��AE=2$\sqrt{3}$��
��$\sqrt{7}$��3��2$\sqrt{3}$��
���������������Ӷ���ʹ�øּܲ��ܻ��
������AC��BF��DF���ɣ�
���������������ܳ��ȵ���Сֵ3$\sqrt{7}$��
�ʴ�Ϊ3$\sqrt{7}$��
���� ���⿼�������ε��ȶ��ԡ�ƽ���ߵ����ʡ�ƽ���ı��ε��ж������ʡ����ɶ������ȱ������ε��ж������ʵ�֪ʶ������Ĺؼ������Ӹ����߹��������������Լ�ƽ���ı��Σ������п��������ͣ�

| A�� | 1-$\sqrt{2}$ | B�� | -1 | C�� | 1��$\sqrt{2}$ | D�� | 1$��\sqrt{2}$��-1 |
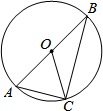 ��ͼ����֪��OΪ��ABC�����Բ����ABΪ��O��ֱ������OC=5��AC=6����BC��Ϊ��������
��ͼ����֪��OΪ��ABC�����Բ����ABΪ��O��ֱ������OC=5��AC=6����BC��Ϊ��������| A�� | 10 | B�� | 9 | C�� | 8 | D�� | ��ȷ�� |
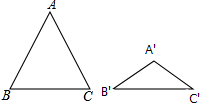 ��ͼ����ABC���A��B��C�䶼�ǵ��������Σ���AB=AC=5��A��B��=A��C��=3������B+��B��=90�㣬���ABC���A��B��C��������Ϊ��������
��ͼ����ABC���A��B��C�䶼�ǵ��������Σ���AB=AC=5��A��B��=A��C��=3������B+��B��=90�㣬���ABC���A��B��C��������Ϊ��������| A�� | 25��9 | B�� | 5��3 | C�� | $\sqrt{5}$��$\sqrt{3}$ | D�� | 5$\sqrt{5}$��3$\sqrt{3}$ |
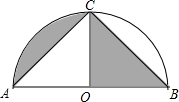 ��ͼ����ABΪֱ������OΪԲ�ĵİ�Բ������C����AC=BC=$\sqrt{2}$����ͼ����Ӱ���ֵ�����ǣ�������
��ͼ����ABΪֱ������OΪԲ�ĵİ�Բ������C����AC=BC=$\sqrt{2}$����ͼ����Ӱ���ֵ�����ǣ�������| A�� | $\frac{��}{4}$ | B�� | $\frac{1}{2}$$+\frac{��}{4}$ | C�� | $\frac{��}{2}$ | D�� | $\frac{1}{2}$+$\frac{��}{2}$ |
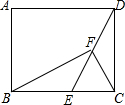 ��ͼ������ABCD�У���EΪBC��һ�㣬FΪDE���е㣬�ҡ�BFC=90�㣮
��ͼ������ABCD�У���EΪBC��һ�㣬FΪDE���е㣬�ҡ�BFC=90�㣮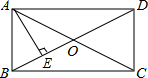 ��ͼ���ھ���ABCD�У�AB=3���Խ���AC��BD�ཻ�ڵ�O��AE��ֱƽ��OB�ڵ�E����AD�ij�Ϊ3$\sqrt{3}$��
��ͼ���ھ���ABCD�У�AB=3���Խ���AC��BD�ཻ�ڵ�O��AE��ֱƽ��OB�ڵ�E����AD�ij�Ϊ3$\sqrt{3}$��