题目内容
13.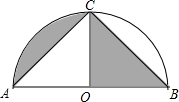 如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是( )
如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是( )| A. | $\frac{π}{4}$ | B. | $\frac{1}{2}$$+\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{1}{2}$+$\frac{π}{2}$ |
分析 先利用圆周角定理得到∠ACB=90°,则可判断△ACB为等腰直角三角形,接着判断△AOC和△BOC都是等腰直角三角形,于是得到S△AOC=S△BOC,然后根据扇形的面积公式计算图中阴影部分的面积.
解答 解:∵AB为直径,
∴∠ACB=90°,
∵AC=BC=$\sqrt{2}$,
∴△ACB为等腰直角三角形,
∴OC⊥AB,
∴△AOC和△BOC都是等腰直角三角形,
∴S△AOC=S△BOC,OA=$\frac{\sqrt{2}}{2}$AC=1,
∴S阴影部分=S扇形AOC=$\frac{90•π•{1}^{2}}{360}$=$\frac{π}{4}$.
故选A.
点评 本题考查了扇形面积的计算:圆面积公式:S=πr2,(2)扇形:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.求阴影面积常用的方法:①直接用公式法; ②和差法; ③割补法.求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
3.对于两个不相等的示数a,b,我们规定符号Max{a,b}表示a、b中的较大值,如:Max{2,4}=4,按照这个规定,方程Max{x,-x}=$\frac{2x+1}{x}$的解为( )
| A. | 1+$\sqrt{2}$或-1 | B. | 2-$\sqrt{2}$ | C. | 1+$\sqrt{2}$或1-$\sqrt{2}$ | D. | 1-$\sqrt{2}$或-1 |
8.甲箱内有4颗球,颜色分别为红、黄、绿、蓝;乙箱内有3颗球,颜色分别为红、黄、黑.小赖打算同时从甲、乙两个箱子中各抽出一颗球,若同一箱中每球被抽出的机会相等,则小赖抽出的两颗球颜色相同的机率为何?( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{7}$ | D. | $\frac{7}{12}$ |
5.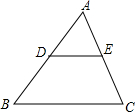 如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( )
如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( )
 如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( )
如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:1 |
3.已知一个正多边形的内角是140°,则这个正多边形的边数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
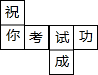 将“祝你考试成功”这六个字分别写在一个正方体的六个面上.若这个正方体的展开图如图所示,则在这个正方体中,与“你”字相对的字是( )
将“祝你考试成功”这六个字分别写在一个正方体的六个面上.若这个正方体的展开图如图所示,则在这个正方体中,与“你”字相对的字是( )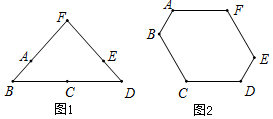 由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)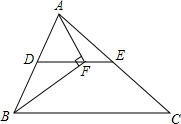 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )
如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )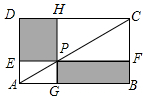 如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.
如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.