题目内容
12.若解关于x的方程$\frac{x+3}{x-1}=\frac{m+1}{x-1}$产生增根,则m的值为3.分析 首先解分式方程,进而利用分式方程无解得出m的值,即可得出答案.
解答 解:方程两边同乘x-1得:x+3=m+1,
解得:x=m-2,方程$\frac{x+3}{x-1}=\frac{m+1}{x-1}$产生增根,
当x-1=0,即x=1时,方程$\frac{x+3}{x-1}=\frac{m+1}{x-1}$产生增根,
∴m-2=1,
∴m=3.
故答案为:3.
点评 此题主要考查了分式方程的解,正确解分式方程再分类讨论是解题关键.

练习册系列答案
相关题目
3.对于两个不相等的示数a,b,我们规定符号Max{a,b}表示a、b中的较大值,如:Max{2,4}=4,按照这个规定,方程Max{x,-x}=$\frac{2x+1}{x}$的解为( )
| A. | 1+$\sqrt{2}$或-1 | B. | 2-$\sqrt{2}$ | C. | 1+$\sqrt{2}$或1-$\sqrt{2}$ | D. | 1-$\sqrt{2}$或-1 |
7.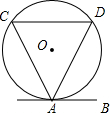 如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
 如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 5 | D. | 6 |
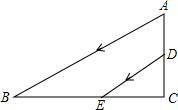 如图,AB、DE是一束平行的阳关从教室的窗口AD射入的平面示意图,且阳光AB与地面BC的夹角为30°,阳光在室内地面的影长BE=2$\sqrt{3}$m,窗口的下檐到教室地面的距离DC=1.2m.求窗顶到地面的距离AC的长.
如图,AB、DE是一束平行的阳关从教室的窗口AD射入的平面示意图,且阳光AB与地面BC的夹角为30°,阳光在室内地面的影长BE=2$\sqrt{3}$m,窗口的下檐到教室地面的距离DC=1.2m.求窗顶到地面的距离AC的长.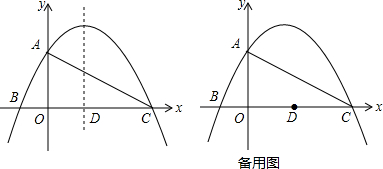
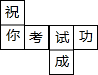 将“祝你考试成功”这六个字分别写在一个正方体的六个面上.若这个正方体的展开图如图所示,则在这个正方体中,与“你”字相对的字是( )
将“祝你考试成功”这六个字分别写在一个正方体的六个面上.若这个正方体的展开图如图所示,则在这个正方体中,与“你”字相对的字是( )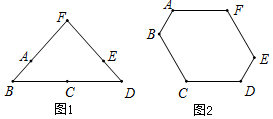 由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)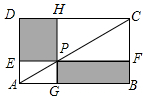 如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.
如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.