题目内容
11．现规定：min（a：b）=$\left\{\begin{array}{l}{b（a＞b）}\\{a（a＜b）}\end{array}\right.$，例如（1：2）=1：min（8：6）=6．按照上面的规定，方程min（x：-x）=$\frac{2x+1}{x}$的根是（ ）| A． | 1-$\sqrt{2}$ | B． | -1 | C． | 1±$\sqrt{2}$ | D． | 1$±\sqrt{2}$或-1 |
分析 根据题中的新定义，分x＜-x与x＞-x两种情况求出所求方程的解即可．
解答 解：当x＜-x，即x＜0时，方程化为x=$\frac{2x+1}{x}$，
去分母得：x2-2x-1=0，
解得：x=$\frac{2±2\sqrt{2}}{2}$=1±$\sqrt{2}$，
即x1=1+$\sqrt{2}$（舍去），x2=1-$\sqrt{2}$，
当x＞-x，即x＞0时，方程化为-x=$\frac{2x+1}{x}$，
去分母得：x2+2x+1=0，即（x+1）2=0，
解得：x1=x2=-1（舍去），
经检验x=1-$\sqrt{2}$是分式方程的解，
综上，所求方程的解为1-$\sqrt{2}$，
故选A．
点评 此题考查了分式方程的解，弄清题中的新定义是解本题的关键．
练习册系列答案
相关题目
1．在平面直角坐标系中，下面的点在第三象限的是（ ）
| A． | （1，2） | B． | （2，-1） | C． | （-2，4） | D． | （-3，-3） |
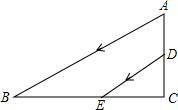如图，AB、DE是一束平行的阳关从教室的窗口AD射入的平面示意图，且阳光AB与地面BC的夹角为30°，阳光在室内地面的影长BE=2$\sqrt{3}$m，窗口的下檐到教室地面的距离DC=1.2m．求窗顶到地面的距离AC的长．
某飞机模型的机翼形状如图所示，其中AB∥DC，∠BAE=90°，根据图中的数据计算CD的长为22cm（精确到1cm）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
如图，在三角形ABC中，B（2，0），把三角形ABC沿AC边平移，使A点到C点，三角形ABC变换为三角形CED，已知C（0，3.5），请写出A，D，E的坐标，并说出平移的过程．
3．对于两个不相等的示数a，b，我们规定符号Max{a，b}表示a、b中的较大值，如：Max{2，4}=4，按照这个规定，方程Max{x，-x}=$\frac{2x+1}{x}$的解为（ ）
| A． | 1+$\sqrt{2}$或-1 | B． | 2-$\sqrt{2}$ | C． | 1+$\sqrt{2}$或1-$\sqrt{2}$ | D． | 1-$\sqrt{2}$或-1 |
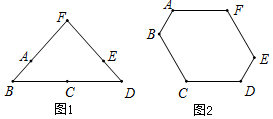由6根钢管首尾顺次铰接而成六边形钢架ABCDEF，相邻两钢管可以转动．已知各钢管的长度为AB=DE=1米，BC=CD=EF=FA=2米．（铰接点长度忽略不计）