题目内容
11.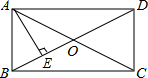 如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为3$\sqrt{3}$.
如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为3$\sqrt{3}$.
分析 由矩形的性质和线段垂直平分线的性质证出OA=AB=OB=3,得出BD=2OB=6,由勾股定理求出AD即可.
解答 解:∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵AE垂直平分OB,
∴AB=AO,
∴OA=AB=OB=3,
∴BD=2OB=6,
∴AD=$\sqrt{B{D}^{2}-A{B}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$;
故答案为:3$\sqrt{3}$.
点评 此题考查了矩形的性质、等边三角形的判定与性质、线段垂直平分线的性质、勾股定理;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
6. 如图,l1∥l2,∠1=56°,则∠2的度数为( )
如图,l1∥l2,∠1=56°,则∠2的度数为( )
 如图,l1∥l2,∠1=56°,则∠2的度数为( )
如图,l1∥l2,∠1=56°,则∠2的度数为( )| A. | 34° | B. | 56° | C. | 124° | D. | 146° |
16.方程$\frac{2x+1}{x-1}$=3的解是( )
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -4 | D. | 4 |
3.已知一个正多边形的内角是140°,则这个正多边形的边数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
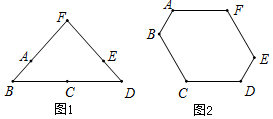 由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)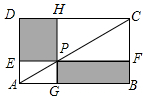 如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.
如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H. “万人马拉松”活动组委会计划制作运动衫分发给参与者,为此,调查了部分参与者,以决定制作橙色、黄色、白色、红色四种颜色运动衫的数量.根据得到的调查数据,绘制成如图所示的扇形统计图.若本次活动共有12000名参与者,则估计其中选择红色运动衫的约有2400名.
“万人马拉松”活动组委会计划制作运动衫分发给参与者,为此,调查了部分参与者,以决定制作橙色、黄色、白色、红色四种颜色运动衫的数量.根据得到的调查数据,绘制成如图所示的扇形统计图.若本次活动共有12000名参与者,则估计其中选择红色运动衫的约有2400名.