题目内容
10.先化简:$\frac{{x}^{2}+x}{{x}^{2}-2x+1}$÷($\frac{2}{x-1}$-$\frac{1}{x}$),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值.分析 先将原分式进行化解,化解过程中注意不为0的量,根据不为0的量结合x的取值范围得出合适的x的值,将其代入化简后的代数式中即可得出结论.
解答 解:$\frac{{x}^{2}+x}{{x}^{2}-2x+1}$÷($\frac{2}{x-1}$-$\frac{1}{x}$)
=$\frac{x(x+1)}{(x-1)^{2}}$÷$\frac{2x-(x-1)}{x(x-1)}$
=$\frac{x(x+1)}{(x-1)^{2}}$×$\frac{x(x-1)}{x+1}$
=$\frac{{x}^{2}}{x-1}$.
其中$\left\{\begin{array}{l}{{x}^{2}-2x+1≠0}\\{(x-1)x≠0}\\{x+1≠0}\end{array}\right.$,即x≠-1、0、1.
又∵-2<x≤2且x为整数,
∴x=2.
将x=2代入$\frac{{x}^{2}}{x-1}$中得:$\frac{{x}^{2}}{x-1}$=$\frac{{2}^{2}}{2-1}$=4.
点评 本题考查了分式的化解求值,解题的关键是找出x的值.本题属于基础题,难度不大,解决该题型题目时,先将原分式进行化简,再代入数据求值即可.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
5.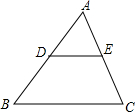 如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( )
如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( )
 如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( )
如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:1 |
15.一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )


| A. | ($\frac{1}{2}$)2015 | B. | ($\frac{1}{2}$)2016 | C. | ($\frac{\sqrt{3}}{3}$)2016 | D. | ($\frac{\sqrt{3}}{3}$)2015 |
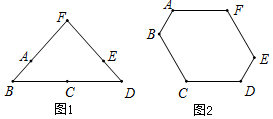 由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)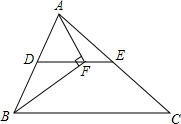 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )
如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )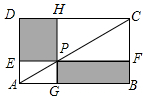 如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.
如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H. “万人马拉松”活动组委会计划制作运动衫分发给参与者,为此,调查了部分参与者,以决定制作橙色、黄色、白色、红色四种颜色运动衫的数量.根据得到的调查数据,绘制成如图所示的扇形统计图.若本次活动共有12000名参与者,则估计其中选择红色运动衫的约有2400名.
“万人马拉松”活动组委会计划制作运动衫分发给参与者,为此,调查了部分参与者,以决定制作橙色、黄色、白色、红色四种颜色运动衫的数量.根据得到的调查数据,绘制成如图所示的扇形统计图.若本次活动共有12000名参与者,则估计其中选择红色运动衫的约有2400名.