Question

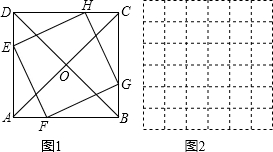
阅读材料：
小强遇到这样一个问题：已知正方形ABCD的边长为a，求作另一个正方形EFGH，使它的四个顶点分别在已知正方形的四条边上，并且边长等于b．
小强的思考是：如图1，假设正方形EFGH已作出，其边长为b，点E、F、G、H分别在AD、AB、BC、CD上，则正方形EFGH的中心就是正方形ABCD的中心O（对角线的交点）．
∵正方形EFGH的边长为b，∴对角线EG=HF=

2

b，
∴OE=OF=OG=OH=

2

2

b，进而点E、F、G、H可作出．
解决问题：
（1）下列网格每个小正方形的边长都为1，请你在图2网格中作出一个正方形ABCD，使它的边长a=

10

，要求A、B、C、D四个顶点都在小正方形的格点上．
（2）参考小强的思路，探究解决下列问题：作另一个正方形EFGH，使它的四个顶点分别在（1）中所作正方形ABCD的边上，并且边长b取得最小值．请你画出图形，并简要说明b取得最小值的理由，写出b的最小值．

Answer 1

考点：四边形综合题

专题：

分析：（1）直接根据勾股定理画出正方形ABCD即可；
（2）取正方形ABCD各边的中点，再顺次连接即可得出正方形EFGH．

解答：解：（1）如图1所示；

（2）如图2所示．b取得最小值的理由：
∵由正方形的中心O向正方形的一边作所有线段中，垂线段OH最短，
∴延长HO交AB边于点F，以FH为一条对角线所做正方形EFGH的边长b就最小，b的最小值为

5

．

点评：本题考查的是四边形综合题，熟知正方形的性质及勾股定理是解答此题的关键．