题目内容
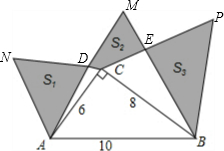
 如图,分别以直角三角形ABC的三边作正三角形,已知AC=6,AB=10,阴影部分的面积分别记为S1,S2,S3,则S1+S3-S2的值为( )
如图,分别以直角三角形ABC的三边作正三角形,已知AC=6,AB=10,阴影部分的面积分别记为S1,S2,S3,则S1+S3-S2的值为( )| A、24 | ||
| B、48 | ||
C、25
| ||
D、50
|
考点:勾股定理
专题:
分析:首先求出△ABM、△ACN、△BCP,设出S△ACD=α,S△BCE=β,S△ABC=γ,证明S1+S3-S2=γ,即可解决问题.
解答:
 解:如图,S△ABM=
解:如图,S△ABM=
×102×sin60°=25
;
同理可求:S△ACN=9
,S△BCP=16
;
设S△ACD=α,S△BCE=β,S△ABC=γ,
则S1+S3-S2=9
-α+16
-β-(25
-α-β-γ)
=9
-α+16
-β-25
+α+β+γ
=γ;
γ=
×6×8=24.
故选A.
 解:如图,S△ABM=
解:如图,S△ABM=| 1 |
| 2 |
| 3 |
同理可求:S△ACN=9
| 3 |
| 3 |
设S△ACD=α,S△BCE=β,S△ABC=γ,
则S1+S3-S2=9
| 3 |
| 3 |
| 3 |
=9
| 3 |
| 3 |
| 3 |
=γ;
γ=
| 1 |
| 2 |
故选A.
点评:该题主要考查了勾股定理、等边三角形等性质等几何知识点及其应用问题;解题的关键是牢固掌握勾股定理、等边三角形等性质等几何知识点.

练习册系列答案
相关题目
利用配方法将x2+2x+3=0化为a(x-h)2+k=0(a≠0)的形式为( )
| A、(x-1)2-2=0 |
| B、(x-1)2+2=0 |
| C、(x+1)2+2=0 |
| D、(x+1)2-2=0 |
下列命题中,真命题是( )
| A、相等的角是对顶角 |
| B、两边及一角分别相等的两个三角形全等 |
| C、直角三角形的任意两角互余 |
| D、两角及其夹边分别相等的两个三角形全等 |
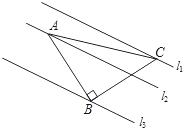 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为3,则AC的长是( )
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为3,则AC的长是( )A、
| ||
B、
| ||
C、
| ||
| D、5 |
图字母所代表的正方形的面积为144的选项为( )
A、 |
B、 |
C、 |
D、 |
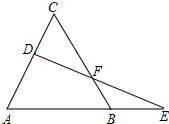 如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F.
如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F. 二次函数y=ax2+bx+c(a≠0)的图象如图,则函数值y>0时,x的取值范围是
二次函数y=ax2+bx+c(a≠0)的图象如图,则函数值y>0时,x的取值范围是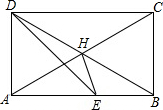 如图,在矩形ABCD中,对角线DB=2AD,DE平分∠CDA,求∠HED的度数.
如图,在矩形ABCD中,对角线DB=2AD,DE平分∠CDA,求∠HED的度数.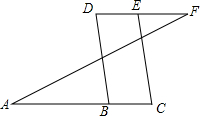 如图,已知∠A=∠F=40°,∠C=∠D=70°,则∠ABD=
如图,已知∠A=∠F=40°,∠C=∠D=70°,则∠ABD=