题目内容
先化简,再求值:
•(1+
)÷
,其中m满足
m-2=4
.
| m-4 |
| m2-9 |
| 14m-7 |
| m2-8m+16 |
| 1 |
| m-3 |
| 2 |
| 2 |
考点:分式的化简求值
专题:计算题
分析:原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把m的值代入计算即可求出值.
解答:
解:原式=
•
•(m-3)
=
•
•(m-3)
=
,
∵
m-2=4
,
∴m=4+
,
则原式=
=6
-5.
| m-4 |
| (m+3)(m-3) |
| m2-8m+16+14m-7 |
| (m-4)2 |
=
| m-4 |
| (m+3)(m-3) |
| (m+3)2 |
| (m-4)2 |
=
| m+3 |
| m-3 |
∵
| 2 |
| 2 |
∴m=4+
| 2 |
则原式=
4+
| ||
4+
|
| 2 |
点评:此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
利用配方法将x2+2x+3=0化为a(x-h)2+k=0(a≠0)的形式为( )
| A、(x-1)2-2=0 |
| B、(x-1)2+2=0 |
| C、(x+1)2+2=0 |
| D、(x+1)2-2=0 |
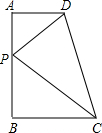 如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=2,AB=6,BC=6,点P是AB上一个动点,则PC+PD的最小值为
如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=2,AB=6,BC=6,点P是AB上一个动点,则PC+PD的最小值为 芳芳的妈妈到白佛某市场去买菜,发现把2.5千克的芹菜放到如图所示的度盘秤上时,指针盘上的指针顺时针旋转了90°,由于芹菜和油麦菜的价钱一样,芳芳的妈妈挑选了一些油麦菜放到仍盛有芹菜的度盘秤上,此时的指针又顺时针旋转了108°,则芳芳的妈妈购买的芹菜和油麦菜的总质量为( )
芳芳的妈妈到白佛某市场去买菜,发现把2.5千克的芹菜放到如图所示的度盘秤上时,指针盘上的指针顺时针旋转了90°,由于芹菜和油麦菜的价钱一样,芳芳的妈妈挑选了一些油麦菜放到仍盛有芹菜的度盘秤上,此时的指针又顺时针旋转了108°,则芳芳的妈妈购买的芹菜和油麦菜的总质量为( )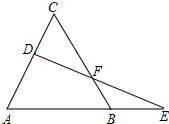 如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F.
如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F.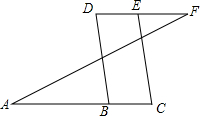 如图,已知∠A=∠F=40°,∠C=∠D=70°,则∠ABD=
如图,已知∠A=∠F=40°,∠C=∠D=70°,则∠ABD=