题目内容
 已知,在△ABC中,∠BAC=135°,AD⊥BC,AD=2,BD=3,求DC的长.
已知,在△ABC中,∠BAC=135°,AD⊥BC,AD=2,BD=3,求DC的长.考点:勾股定理,等腰直角三角形
专题:
分析:如图,首先证明AD=DC;运用勾股定理和三角函数的定义列出方程22+μ2=2λ2①、
=
②,联立①②并解得μ=10,即可解决问题.
| 2 | ||
|
| λ |
| 3+μ |
解答:
 解:如图,过点C作CD⊥BA,交BA的延长线于点D;
解:如图,过点C作CD⊥BA,交BA的延长线于点D;
∵∠BAC=135°,
∴∠DAC=45°,∠DCA=90°-45°=45°,
∴AD=DC(设为λ),设CD=μ;
由勾股定理得:AC2=AD2+DC2=AD2+DC2,
即22+μ2=2λ2①;AB=
=
;
∵sinB=
=
,
∴
=
②,联立①②得:5μ2-48μ-20=0,
解得:μ=10,或-
(舍去),
即DC的长为10.
 解:如图,过点C作CD⊥BA,交BA的延长线于点D;
解:如图,过点C作CD⊥BA,交BA的延长线于点D;∵∠BAC=135°,
∴∠DAC=45°,∠DCA=90°-45°=45°,
∴AD=DC(设为λ),设CD=μ;
由勾股定理得:AC2=AD2+DC2=AD2+DC2,
即22+μ2=2λ2①;AB=
| 22+32 |
| 13 |
∵sinB=
| AD |
| AB |
| CD |
| BC |
∴
| 2 | ||
|
| λ |
| 3+μ |
解得:μ=10,或-
| 2 |
| 5 |
即DC的长为10.
点评:该题主要考查了勾股定理、等腰直角三角形的性质等几何知识点及其应用问题;解题的关键是牢固掌握勾股定理、等腰直角三角形的性质等几何知识点.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 芳芳的妈妈到白佛某市场去买菜,发现把2.5千克的芹菜放到如图所示的度盘秤上时,指针盘上的指针顺时针旋转了90°,由于芹菜和油麦菜的价钱一样,芳芳的妈妈挑选了一些油麦菜放到仍盛有芹菜的度盘秤上,此时的指针又顺时针旋转了108°,则芳芳的妈妈购买的芹菜和油麦菜的总质量为( )
芳芳的妈妈到白佛某市场去买菜,发现把2.5千克的芹菜放到如图所示的度盘秤上时,指针盘上的指针顺时针旋转了90°,由于芹菜和油麦菜的价钱一样,芳芳的妈妈挑选了一些油麦菜放到仍盛有芹菜的度盘秤上,此时的指针又顺时针旋转了108°,则芳芳的妈妈购买的芹菜和油麦菜的总质量为( )| A、3千克 | B、4.5千克 |
| C、5.5千克 | D、6.5千克 |
 十一国庆期间,保龙仓超市对A,B两种型号的整理箱进行促销,促销价格如图所示,慧慧(其为会员)在该超市进行促销期间购买了2个A型号整理箱,3个B型号整理箱,若a=5,则慧慧总共花费( )
十一国庆期间,保龙仓超市对A,B两种型号的整理箱进行促销,促销价格如图所示,慧慧(其为会员)在该超市进行促销期间购买了2个A型号整理箱,3个B型号整理箱,若a=5,则慧慧总共花费( )| A、143.5元 |
| B、144.5元 |
| C、168.5元 |
| D、169.5元 |
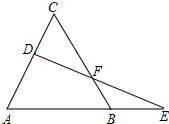 如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F.
如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F. 在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,证明:BE2+CF2=EF2.
在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,证明:BE2+CF2=EF2. 二次函数y=ax2+bx+c(a≠0)的图象如图,则函数值y>0时,x的取值范围是
二次函数y=ax2+bx+c(a≠0)的图象如图,则函数值y>0时,x的取值范围是