题目内容
将一颗骰子（正方体）连掷两次，得到的点数都是4的概率是 ．
考点：列表法与树状图法
专题：
分析：首先根据题意列出表格，然后由表格即可求得所有等可能的结果与得到的点数都是4的情况，再利用概率公式即可求得答案．
解答：
解：列表得：
∵一共有36种等可能的情况，它们的点数都是4的有1种情况，
∴点数都是4的概率是：
．
故答案为：
．
| （1，6） | （2，6） | （3，6） | （4，6） | （5，6） | （6，6） |
| （1，5） | （2，5） | （3，5） | （4，5） | （5，5） | （6，5） |
| （1，4） | （2，4） | （3，4） | （4，4） | （5，4） | （6，4） |
| （1，3） | （2，3） | （3，3） | （4，3） | （5，3） | （6，3） |
| （1，2） | （2，2） | （3，2） | （4，2） | （5，2） | （6，2） |
| （1，1） | （2，1） | （3，1） | （4，1） | （5，1） | （6，1） |
∴点数都是4的概率是：
| 1 |
| 36 |
故答案为：
| 1 |
| 36 |
点评：此题考查了树状图法与列表法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
计算：
-3÷（-
）×2+（-2）-2=（ ）
| 2 | ||
|
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、14-
| ||||
D、
|
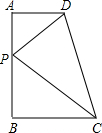如图所示，在直角梯形ABCD中，∠ABC=90°，AD∥BC，AD=2，AB=6，BC=6，点P是AB上一个动点，则PC+PD的最小值为利用配方法将x2+2x+3=0化为a（x-h）2+k=0（a≠0）的形式为（ ）
| A、（x-1）2-2=0 |
| B、（x-1）2+2=0 |
| C、（x+1）2+2=0 |
| D、（x+1）2-2=0 |
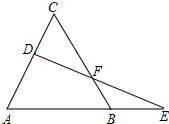如图，已知△ABC是等边三角形，D为AC上一个动点，延长AB至E，使BE=CD，连接DE交BC于点F．