��Ŀ����
��ͼ�� 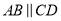 ��
�� 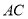 ��
�� 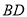 ����
����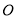 ��
�� 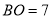 ��
�� 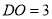 ��
�� 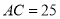 ����
����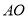 ���� ����
���� ����
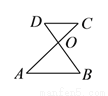
A. 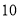 B.
B. 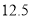 C.
C. 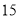 D.
D. 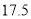
��������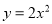 ������ƽ��һ����λ��������ƽ��һ����λ������ƽ�ƺ�õ��������߽���ʽΪ�� ����
������ƽ��һ����λ��������ƽ��һ����λ������ƽ�ƺ�õ��������߽���ʽΪ�� ����
A. 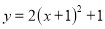 B.
B. 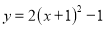 C.
C. 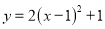 D.
D. 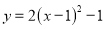
�����κ���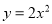 ��ͼ����
��ͼ����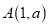 ����
����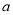 ��ֵΪ�� ����
��ֵΪ�� ����
A. 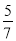 B.
B. 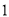 C.
C. 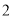 D.
D. 
��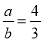 ����
����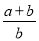 ��ֵ���ڣ� ����
��ֵ���ڣ� ����
A. 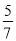 B.
B. 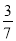 C.
C. 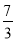 D.
D. 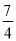
�����������
ѧϰ��������ȫ�ȵ��ж�����������SSS������ASA������AAS������SSS������ֱ��������ȫ�ȵ��ж�����������HL���������Ǽ����ԡ������������������ߺ�����һ�ߵĶԽǶ�Ӧ��ȡ������ν����о���
������˼����
���Dz����������÷������Ա�ʾΪ���ڡ�ABC�͡�DEF�У�AC=DF��BC=EF����B=��E��Ȼ�ԡ�B���з��࣬�ɷ�Ϊ����B��ֱ�ǡ��۽ǡ���ǡ������������̽����
������̽����
��һ�����������B��ֱ��ʱ����ABC�ա�DEF��
��ͼ�٣��ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E=90�㣬������ ��������֪��Rt��ABC��Rt��DEF��
�ڶ������������B�Ƕ۽�ʱ����ABC�ա�DEF��
��ͼ�ڣ��ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E���ҡ�B����E���Ƕ۽ǣ�����֤������ABC�ա�DEF����ʾ������C��CG��AB��AB���ӳ�����G������F��FH��DE��DE���ӳ�����H����
���������������B�����ʱ����ABC�͡�DEF��һ��ȫ�ȣ�
�ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E���ҡ�B����E������ǣ���������ͼ�ۣ���ͼ�����ó߹�������DEF��ʹ��DEF�͡�ABC��ȫ�ȣ�
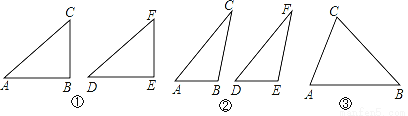
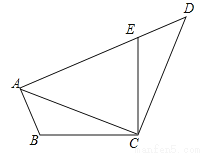
��ͼ����֪���ı���ABCD�У���E��AD�ϣ���BCE=��ACD=90�㣬��BAC=��D��BC=CE��
��1����֤��AC=CD��
��2����AC=AE�����DEC�Ķ�����
- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��|x|=4��|y|=7����x+y��0����ôx��y��ֵ�ǣ�������
A. 3��11 B. 3��11 C. ��3��11 D. ��3��11
D �����������ݾ���ֵ�����ʣ���֪x=��4��y����7��Ȼ�����x+y��0����֪x=4��y=7��x=-4��y=7�����x-y=4-7=-3��x-y=-4-7=-11. ��ѡ��D.������һ��A��һֻ���ϴ�A��������4����λ���ȵ���ԭ�㣬���A����ʾ�����ǣ�������
A. 4 B. ��4 C. ��8 D. ��4
�鿴��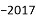
A. 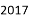
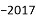
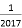 D.
D. 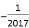
��֪����ʽA��B������A��B��ijͬѧ������ʱ��A��B������A+B���������ΪA+B=3m2��2m��5����B=2m2��3m��2����������������ȷ�𰸣�
�鿴����֪|a��2|+��b+1��2=0����5ab2��|2a2b����4ab2��2a2b��|��ֵ��
�鿴�����˾������ij������Ӫ��ȫ���ڶ��������ʤ��·�Ͻ��У�����涨��Ϊ��������Ϊ���������������г���̣���λ������ �����£�
+8��+4����10����8��+6����2����5����7��+4��+6����8����9
��1�����ڼ����˿��͵�Ŀ�ĵ�ʱ�������պûص���������㣿
��2�������һ���˿��� ��Ŀ�ĵ�ʱ������������������Զ��
��3��������������Ϊ0.4��/������������������Ͷ�������
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ�����
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ,��֪C���߶�AB�ϵ�����һ��(�˵����),�ֱ���AC,BCΪ�߲�����AB��ͬһ�����ȱ�������ACD�͵ȱ�������BCE,����AE��CD�ڵ�M,����BD��CE�ڵ�N.����������������:
��AE=BD;��CN=CM;��MN��AB.������ȷ���۵ĸ�����(����)
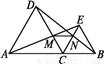
A. 0 B. 1 C. 2 D. 3
D ������������������ߡ�ACD�͡�BCE�ǵȱ������Σ� ���ACD=��BCE=60�㣬AC=DC��EC=BC�� ���ACD+��DCE=��DCE+��ECB�� ����ACE=��DCB�� ���ACE�ա�DCB��SAS���� ��AE=BD���ʢ���ȷ�� ���EAC=��NDC�� �ߡ�ACD=��BCE=60�㣬 ���DCE=60�㣬 ���ACD=��MCN=60�㣬 ��AC=DC�� ���...С����үүÿ��������������ij������������ҽ�Զ���̵���������һ���̫��ȭ���ܲ��ؼң������ܷ�ӳ����С����үү��ҵľ���y��ʱ��x�ĺ�����ϵ�Ĵ���ͼ���ǣ� ����
A. 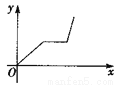 B.
B. 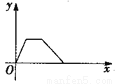 C.
C. 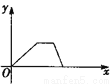 D.
D. 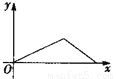
��һ��ͼ��������һ��ֱ�߽�����ԳƱ任��������������ֱ��ƽ�еķ���ƽ�ƣ����ǰ�������ͼ�α任���������ԳƱ任������Ȼ����ճ������У������ش�������ͼ�α任����ͼ1���������ԳƱ任��ƽ�Ʊ任���й����ʣ�����Ϊ�ڻ����ԳƱ任�����У�������Ӧ�����Σ���ͼ2���Ķ�Ӧ�������е������ǣ��� ����
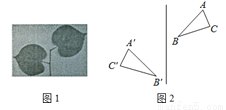
A. ��Ӧ��������Գ��ᴹֱ
B. ��Ӧ�����߱��Գ���ƽ��
C. ��Ӧ�����߱��Գ��ᴹֱƽ��
D. ��Ӧ��������ƽ��
�鿴����ͼ��ij��7��1����10�յĿ�������ָ������ͼ����������ָ��С��100��ʾ����������������������ָ������200��ʾ�����ض���Ⱦ��ij�����ѡ��7��1����7��8���е�ijһ�쵽����У�������ͣ��4�죮������ڸ���ͣ���ڼ����ҽ���1��������������ĸ����ǣ� ��
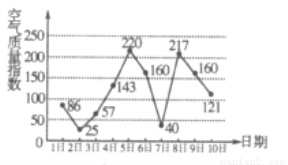
A ��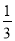 B��
B��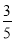 C��
C��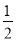 D��
D��
һ��������һ��Ħ�г��ֱ��A��B����ȥͬһ���У�������A�صľ�����ʱ��仯��ͼ����ͼ��ʾ�������н��۴������(����)
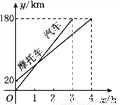
A. Ħ�г�����������1 h B. A��B���صľ���Ϊ20 km
C. Ħ�г����ٶ�Ϊ45 km/h D. �������ٶ�Ϊ60 km/h
�鿴����һЩ�������У��еĺ�������Գ�ͼ�Σ������ĸ������У����Կ�����Գ�ͼ�ε��ǣ� ��
A�� B��
B�� C��
C�� D��
D��
- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ����������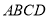 �У�
�У� 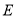 Ϊ�Խ���
Ϊ�Խ���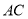 ��
�� 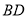 �Ľ��㣬������
�Ľ��㣬������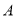 �͵�
�͵�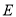 ����
����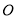 ���ֱ�
���ֱ�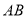 ��
�� 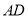 �ڵ�
�ڵ�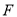 ��
�� 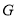 ����֪�����α߳�Ϊ
����֪�����α߳�Ϊ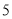 ����
����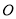 �İ뾶Ϊ
�İ뾶Ϊ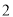 ����
����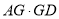 ��ֵΪ__________��
��ֵΪ__________��
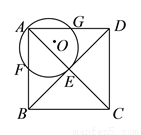
��ͼ��������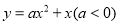 ��
��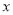 ���ڵ�
���ڵ�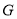 ��
�� 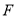 ����
����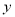 ���ڵ�
���ڵ�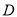 ����
����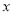 ���Ϸ�����������������
���Ϸ�����������������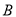 ��
�� 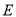 �����ǹ���
�����ǹ���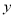 ��Գƣ���
��Գƣ���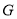 ��
�� 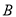 ��
��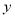 ����࣬
����࣬ 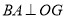 �ڵ�
�ڵ�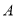 ��
�� 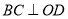 �ڵ�
�ڵ�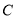 ���ı���
���ı���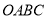 ���ı���
���ı���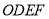 ������ֱ�Ϊ
������ֱ�Ϊ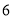 ��
��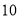 ����
����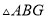 ��
��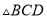 �����֮��Ϊ__________��
�����֮��Ϊ__________��
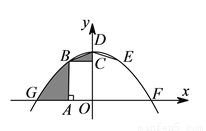
��ͼ����֪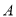 ��
�� 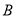 ��
�� 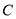 ��
�� 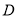 �ǡ�
�ǡ� �ϵ��ĸ��㣬
�ϵ��ĸ��㣬 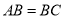 ��
�� 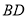 ��
��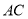 �ڵ�
�ڵ�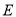 ������
������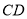 ��
�� 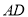 ����
����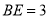 ��
�� 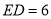 ����
����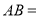 __________��
__________��
��ͼ���� ��
��  ��
��  �ڡ�
�ڡ� �ϣ�
�ϣ� 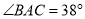 ����
����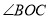 ����__________�ȣ�
����__________�ȣ�

��֪��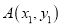 ��
�� 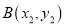 �ڶ��κ���
�ڶ��κ���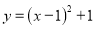 ��ͼ���ϣ���
��ͼ���ϣ���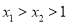 ����
����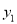 __________
__________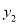 �����
�����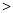 ����
���� 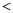 ����
���� 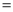 ����
����
���κ���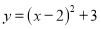 ͼ��Ķ���������__________��
ͼ��Ķ���������__________��
- ���ͣ������
- �Ѷȣ�����
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
���κ���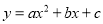 ��ͼ����ͼ��ʾ��������
��ͼ����ͼ��ʾ��������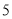 �����ۣ���
�����ۣ���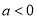 ����
����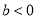 ����
����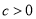 ����
����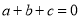 ����
����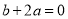 �У���������ȷ���У� ����
�У���������ȷ���У� ����
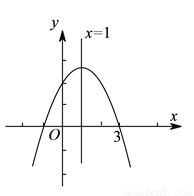
A. �٢ۢ� B. �ڢܢ� C. �٢ڢ� D. �٢ۢ�
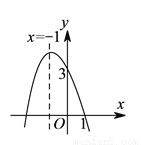
D ���������ɺ���ͼ���֪�������߿������£���a<0����ѡ�����ȷ�� �߶Գ�����y���ұߣ���x=?=1>0�� ��a<0����b>0����ѡ��ڴ��� ����������y�ύ����y�������ᣬ��c>0����ѡ�����ȷ�� ��x=1ʱ����Ӧ��ͼ���ϵĵ���x���Ϸ�����y=ax2+bx+c=a+b+c>0����ѡ��ܴ��� ��x=?=1���εã�2a+b=0����ѡ�����ȷ�� ���ϣ���...������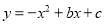 �IJ���ͼ����ͼ��ʾ����
�IJ���ͼ����ͼ��ʾ����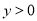 ����
����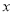 ��ȡֵ��Χ�ǣ� ����
��ȡֵ��Χ�ǣ� ����
A. 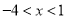 B.
B. 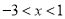 C.
C. 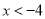 ��
��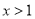 D.
D. 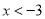 ��
��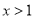
��ͼ����֪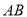 �ǡ�
�ǡ�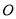 ��ֱ��������
��ֱ��������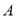 ����
����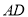 ƽ���ڰ뾶
ƽ���ڰ뾶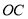 ����
����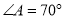 ����
����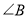 ���ڣ� ����
���ڣ� ����

A. 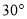 B.
B. 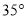 C.
C. 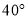 D.
D. 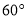
��ƽ��ֱ������ϵ�У�����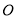 ����ԭ��ΪԲ�ģ�
����ԭ��ΪԲ�ģ� 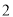 Ϊ�뾶��Բ�����
Ϊ�뾶��Բ�����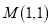 �ڣ� ����
�ڣ� ����
A. ��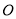 �� B. ��
�� B. ��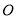 �� C. ��
�� C. ��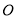 �� D. ����ȷ��
�� D. ����ȷ��
��ͼ����֪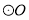 �İ뾶
�İ뾶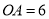 ��
�� 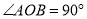 ����
����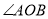 ���ԵĻ�
���ԵĻ�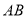 �ij�Ϊ�� ��
�ij��� ��
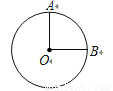
A. 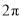 B.
B. 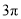 C.
C. 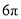 D.
D. 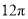
��ͼ�� 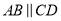 ��
�� 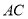 ��
�� 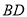 ����
����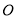 ��
�� 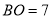 ��
�� 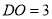 ��
�� 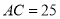 ����
����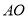 ���� ����
���� ����
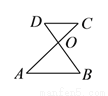
A. 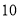 B.
B. 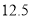 C.
C. 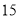 D.
D. 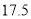
- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ����֪���ı���ABCD�У���E��AD�ϣ���BCE=��ACD=90�㣬��BAC=��D��BC=CE��
��1����֤��AC=CD��
��2����AC=AE�����DEC�Ķ�����

��ͼ����ֱ������ƽ���ڣ���֪��A��8��0������B��3��0������C�ǵ�A����ֱ��m��ֱ��m�ϸ���ĺ����궼Ϊ3���ĶԳƵ㣮
��1����ͼ�б����A��B��C��λ�ò������C�����ꣻ
��2�������P��y���ϣ�����P��ֱ��l��x�ᣬ��A����ֱ��l�ĶԳƵ��ǵ�D����ô����BCD���������10ʱ�����P�����꣮
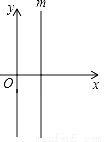
��һ��ֱ�����ǰ���ͼ�ڷţ�����ֱ�ǰ�ABC��б��BC�뺬30��ǵ�ֱ�����ǰ�DBE��ֱ�DZ�BD������ͬ����б��BC��BE��ͬһֱ���ϣ�AC��BD���ڵ�O������CD��
��֤����CDO�ǵ��������Σ�
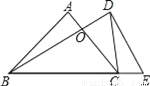
��ͼ����ABC�͡�ADE�ǵȱ������Σ�AD��BC���ϵ����ߣ���֤��BE=BD��
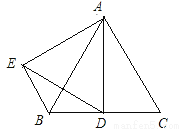
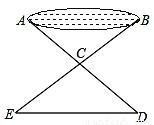
��ͼ����C��F��E��B��һ��ֱ���ϣ���CFD����BEA��CE��BF��DF��AE��д��CD��AB֮��Ĺ�ϵ����֤����Ľ��ۣ�
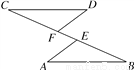
��ͼ���ڡ�ABC�У�CD��AB���ϸߣ�BEΪ��ƽ���ߣ�����BFC=113�㣬���BCF�Ķ�����
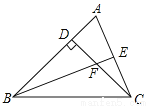
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ���ڡ�ABC�У���D��BC����AB=AD��AC=AE����BAD=��CAE��DE=12��CD=4����BD=_________��
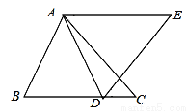
���������ε�һ���ڽ�Ϊ80�㣬�ǵĶ�����_________��
�鿴����ͼ��ABC�У���A����B=1��2��DE��AB��E���ҡ�FCD=75�㣬���D=________��
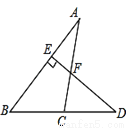
��ͼ��Ҫ������������A��B�ľ��룬������ƽ����ȡһ������ֱ�ӵ���A��B�����C������AC���ӳ�AC����D��ʹCD=CA������BC���ӳ�BC����E��ʹCE=CB������DE����ô����DE�ij��͵���AB�ij���������Ϊ��ABC�ա�DEC��������ж�ȫ�ȵ�������____________��
��ͼ����֪��BDΪ��ABC�Ľ�ƽ���ߣ���BD=BC��EΪBD�ӳ����ϵ�һ�㣬BE=BA��������ۣ��١�ABD�ա�EBC����AC=2CD����AD=AE=EC���ܡ�BCE+��BCD=180�㣮������ȷ���ǣ�������
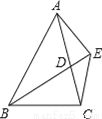
A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �ڢۢ�
�鿴����֪���ڡ�ABC�У���A=60�㣬��Ҫ�ж���ABC�ǵȱ������Σ���������һ��������������������˵����
���������������AB=AC������ô��ABC�ǵȱ������Σ�
�����������������B=��C������ô��ABC�ǵȱ������Σ�
�����������������AB��BC�ϵĸ���ȡ�����ô��ABC�ǵȱ������Σ�
����˵���У���ȷ���У�������
A. 3�� B. 2�� C. 1�� D. 0��
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������

