题目内容
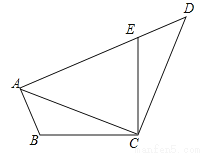
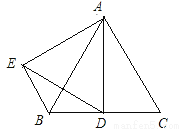
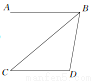
如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于直线m(直线m上各点的横坐标都为3)的对称点.
(1)在图中标出点A,B,C的位置并求出点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于10时,求点P的坐标.
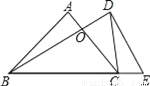
将一副直角三角板如图摆放,等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.
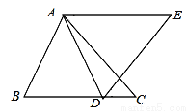
如图:△ABC和△ADE是等边三角形,AD是BC边上的中线.求证:BE=BD.
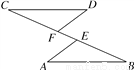
如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.
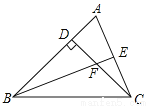
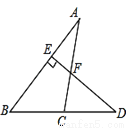
如图,在△ABC中,CD是AB边上高,BE为角平分线,若∠BFC=113°,求∠BCF的度数.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案出租车司机老李某天上午营运全是在东西走向的胜利路上进行,如果规定向东为正,向西为负,他这天上午行车里程(单位:公里 )如下:
+8,+4,﹣10,﹣8,+6,﹣2,﹣5,﹣7,+4,+6,﹣8,﹣9
(1)将第几名乘客送到目的地时,老王刚好回到上午出发点?
(2)将最后一名乘客送 到目的地时,老王距上午出发点多远?
(3)若汽车耗油量为0.4升/公里,这天上午老王耗油多少升?
(1)5;(2)21;(3)30.8. 【解析】试题分析:(1)根据题意求和即可; (2)根据题意求和即可; (3)求出所有路程的绝对值的和,再乘以每公里耗油量即可. 试题解析:(1)∵+8+4-10-8+6=0 ∴将第五名乘客送到目的地时,老王刚好回到上午出发点. (2)将最后一名乘客送到目的地时,老王距上午出发点的距离为:+8+4-10-8+6-2-5-7+...先化简,再求值.
(1)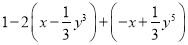 ,其中x=﹣
,其中x=﹣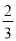 ,y=﹣1.
,y=﹣1.
(2)﹣a2b+(3ab2﹣a2b)﹣2(2ab2﹣a2b),其中a=1,b=﹣2.
查看答案若有理数m、n在数轴上的位置如图所示,请化简:|m+n|+|m﹣n|﹣|n|.
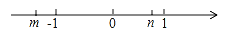
在数轴上有三个点A,B,C,分别表示﹣3,0,2.按下列要求回答:
(1)点A向右移动6个单位后,三个点表示的数谁最大?
(2)点C向左移动3个单位后,这时点B表示的数比点C表示的数大多少?
(3)怎样移动点A,B,C中的两个点,才能使三个点所表示的数相同?有几种办法?分别写出来.
查看答案计算
(1)(﹣3)+(﹣4)﹣(+11)﹣(﹣9);
(2)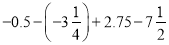 ;
;
(3)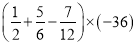 ;
;
(4)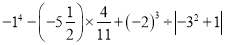 .
.
把下列各数填入相应的大括号内:
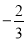 ,
, 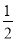 ,﹣0.01,
,﹣0.01, 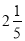 ,7,1,﹣(﹣4),+(﹣1)
,7,1,﹣(﹣4),+(﹣1)
正数集合{ …}
负数集合{ …}
非负整数集合{ …}
分数集合{ …}.
查看答案 试题属性- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
在一些美术字中,有的汉字是轴对称图形,下列四个汉字中,可以看作轴对称图形的是( )
A. B.
B. C.
C. D.
D.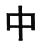
下列四个图形:其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
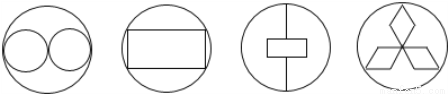
A. 1 B. 2 C. 3 D. 4
查看答案下列说法正确的是( )
A. “任意画出一个等边三角形,它是轴对称图形”是随机事件
B. 某种彩票的中奖率为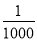 ,说明每买1 000张彩票,一定有一张中奖
,说明每买1 000张彩票,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为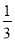
D. “概率为1的事件”是必然事件
查看答案如图所示,AB∥CD,BC平分∠ABD,若∠C=40°,则∠D的度数为 ( )
A. 90° B. 100° C. 110° D. 120°
查看答案下列计算正确的是( )
A. 4x3•2x2=8x6 B. a4+a3=a7 C. (﹣x2)5=﹣x10 D. (a﹣b)2=a2﹣b2
查看答案如图,在平面直角坐标系中,点 ,
,  分别是
分别是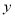 轴正半轴,
轴正半轴, 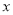 轴正半轴上两动点,
轴正半轴上两动点, 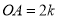 ,
, 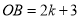 ,以
,以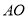 ,
, 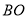 为邻边构造矩形
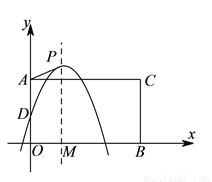
为邻边构造矩形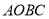 ,抛物线
,抛物线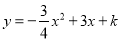 交
交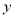 轴于点
轴于点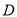 ,
, 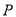 为顶点,
为顶点, 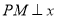 轴于点
轴于点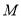 .
.
(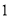 )求
)求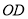 ,
, 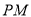 的长(结果均用含
的长(结果均用含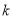 的代数式表示);
的代数式表示);
( )当
)当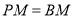 时,求该抛物线的表达式;
时,求该抛物线的表达式;
( )在点
)在点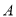 在整个运动过程中,若存在
在整个运动过程中,若存在 是等腰三角形,请求出所有满足条件的
是等腰三角形,请求出所有满足条件的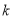 的值.
的值.
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
二次函数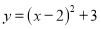 图象的顶点坐标是__________.
图象的顶点坐标是__________.
如图,已知⊙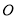 的半径
的半径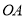 垂直直线
垂直直线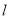 于点
于点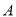 ,点
,点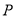 从点
从点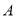 出发,沿直线
出发,沿直线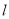 向右运动,同时点
向右运动,同时点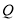 从点
从点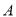 出发沿着圆周按逆时针以相同的速度运动,当点
出发沿着圆周按逆时针以相同的速度运动,当点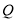 返回到点
返回到点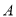 时,点
时,点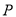 也停止运动.连接
也停止运动.连接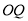 ,
, 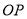 ,则阴影部分面积
,则阴影部分面积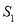 ,
, 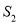 的关系是( ).
的关系是( ).

A. 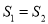 B. 先
B. 先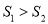 ,再
,再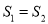 ,最后
,最后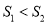
C. 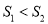 D. 先
D. 先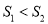 ,再
,再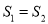 ,再后
,再后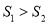
二次函数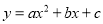 的图象,如图所示,有下列
的图象,如图所示,有下列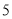 个结论:①
个结论:①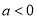 ;②
;②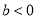 ;③
;③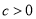 ;④
;④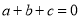 ;⑤
;⑤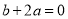 中,则其中正确的有( ).
中,则其中正确的有( ).
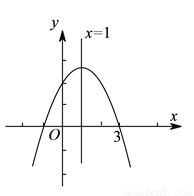
A. ①③④ B. ②④⑤ C. ①②④ D. ①③⑤
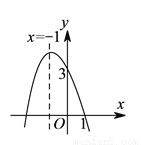
查看答案抛物线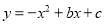 的部分图象如图所示,若
的部分图象如图所示,若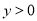 ,则
,则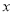 的取值范围是( ).
的取值范围是( ).
A. 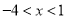 B.
B. 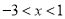 C.
C. 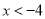 或
或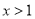 D.
D. 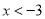 或
或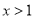
如图,已知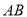 是⊙
是⊙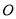 的直径,过点
的直径,过点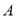 的弦
的弦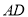 平行于半径
平行于半径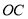 ,若
,若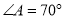 ,则
,则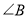 等于( ).
等于( ).

A. 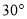 B.
B. 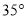 C.
C. 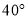 D.
D. 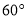
在平面直角坐标系中,若⊙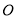 是以原点为圆心,
是以原点为圆心, 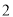 为半径的圆,则点
为半径的圆,则点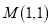 在( ).
在( ).
A. ⊙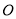 内 B. ⊙
内 B. ⊙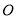 外 C. ⊙
外 C. ⊙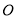 上 D. 不能确定
上 D. 不能确定
- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图, 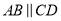 ,
, 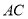 ,
, 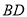 交于
交于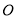 ,
, 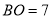 ,
, 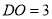 ,
, 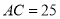 ,则
,则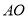 长为( ).
长为( ).
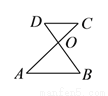
A. 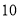 B.
B. 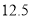 C.
C. 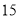 D.
D. 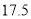
将抛物线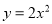 先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
A. 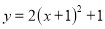 B.
B. 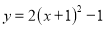 C.
C. 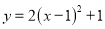 D.
D. 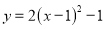
若二次函数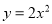 的图象经过点
的图象经过点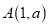 ,则
,则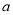 的值为( ).
的值为( ).
A. 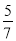 B.
B. 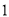 C.
C. 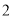 D.
D. 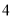
若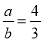 ,则
,则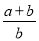 的值等于( ).
的值等于( ).
A. 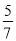 B.
B. 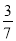 C.
C. 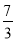 D.
D. 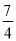
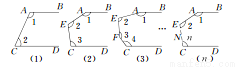
【问题提出】
学习了三角形全等的判定方法(即“SSS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
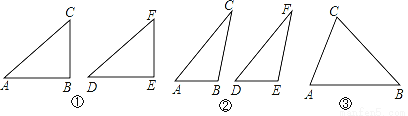
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,请你证明:△ABC≌△DEF(提示:过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H).
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你利用图③,在图③中用尺规作出△DEF,使△DEF和△ABC不全等.
如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在△ABC中,CD是AB边上高,BE为角平分线,若∠BFC=113°,求∠BCF的度数.

如图,△ABC是等边三角形,∠CBD=90°,BD=BC,连接AD交BC于点E,则∠AEC的度数是_________.
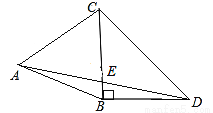
如图,在△ABC中,点D在BC上且AB=AD,AC=AE,∠BAD=∠CAE,DE=12,CD=4,则BD=_________.
等腰三角形的一个内角为80°,则顶角的度数是_________.
查看答案如图△ABC中,∠A:∠B=1:2,DE⊥AB于E,且∠FCD=75°,则∠D=________.
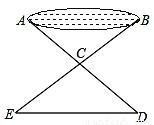
如图,要测量池塘两端A,B的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连接BC并延长BC到点E,使CE=CB,连接DE,那么量出DE的长就等于AB的长,这是因为△ABC≌△DEC,而这个判定全等的依据是____________.
- 题型:解答题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知:在△ABC中,∠A=60°,如要判定△ABC是等边三角形,还需添加一个条件.现有下面三种说法:
①如果添加条件“AB=AC”,那么△ABC是等边三角形;
②如果添加条件“∠B=∠C”,那么△ABC是等边三角形;
③如果添加条件“边AB、BC上的高相等”,那么△ABC是等边三角形.
上述说法中,正确的有( )
A. 3个 B. 2个 C. 1个 D. 0个
A 【解析】有一个角是60°的等腰三角形是等边三角形,①②③都可以说明三角形是等腰三角形,故都正确,故选A如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于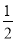 BC的长为半径作弧,两弧相交于两点M,N;
BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
若CD=AC,∠A=50°,则∠ACB的度数为( )
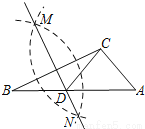
A. 90° B. 95° C. 100° D. 105°
查看答案如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为
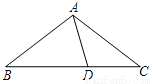
A. 40° B. 36° C. 30° D. 25°
查看答案如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确结论的个数是( )
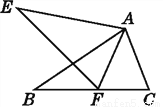
A. 1个 B. 2个 C. 3个 D. 4个
查看答案在平面直角坐标系中.点P(1,﹣2)关于x轴对称的点的坐标是( )
A. (1,2) B. (﹣1,﹣2) C. (﹣1,2) D. (﹣2,1)
查看答案如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于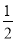 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
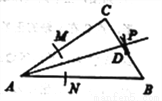
A. 15 B. 30 C. 45 D. 60
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧


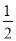 x+9=3x+2的解的是x=______.
x+9=3x+2的解的是x=______.