题目内容
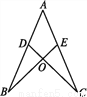
如图,已知C是线段AB上的任意一点(端点除外),分别以AC,BC为边并且在AB的同一侧作等边三角形ACD和等边三角形BCE,连接AE交CD于点M,连接BD交CE于点N.给出以下三个结论:
①AE=BD;②CN=CM;③MN∥AB.其中正确结论的个数是( )
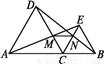
A. 0 B. 1 C. 2 D. 3
D 【解析】试题解析:∵△ACD和△BCE是等边三角形, ∴∠ACD=∠BCE=60°,AC=DC,EC=BC, ∴∠ACD+∠DCE=∠DCE+∠ECB, 即∠ACE=∠DCB, ∴△ACE≌△DCB(SAS), ∴AE=BD,故①正确; ∴∠EAC=∠NDC, ∵∠ACD=∠BCE=60°, ∴∠DCE=60°, ∴∠ACD=∠MCN=60°, ∵AC=DC, ∴△...小华的爷爷每天坚持体育锻炼,某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( ).
A. 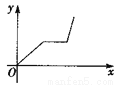 B.
B. 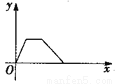 C.
C. 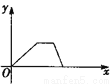 D.
D. 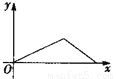
把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是( )
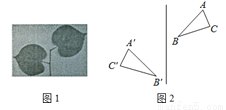
A. 对应点连线与对称轴垂直
B. 对应点连线被对称轴平分
C. 对应点连线被对称轴垂直平分
D. 对应点连线互相平行
查看答案右图是某市7月1日至10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择7月1日至7月8日中的某一天到达该市,并连续停留4天.则此人在该市停留期间有且仅有1天空气质量优良的概率是( )
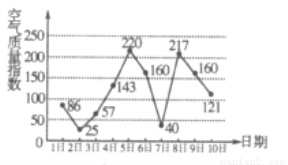
A 、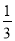 B、
B、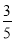 C、
C、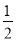 D、
D、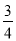
一辆汽车和一辆摩托车分别从A、B两地去同一城市,它们离A地的距离随时间变化的图像如图所示.则下列结论错误的是( )
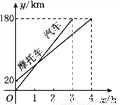
A. 摩托车比汽车晚到1 h B. A、B两地的距离为20 km
C. 摩托车的速度为45 km/h D. 汽车的速度为60 km/h
查看答案在一些美术字中,有的汉字是轴对称图形,下列四个汉字中,可以看作轴对称图形的是( )
A. B.
B. C.
C. D.
D.
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知10m=2,10n=3,则103m+2n=( )
A. 17 B. 72 C. 12 D. 36
B 【解析】试题解析: 故选B.在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开,如图(1),然后拼成一个梯形,如图(2),根据这两个图形的面积关系,表明下列式子成立的是( )
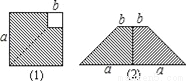
A. a2﹣b2=(a+b)(a﹣b) B. (a+b)2=a2+2ab+b2
C. (a﹣b)2=a2﹣2ab+b2 D. a2﹣b2=(a﹣b)2
查看答案下列因式分解不正确的是( )
A. x2﹣6x+9=(x﹣3)2 B. x2﹣y2=(x﹣y)2
C. x2﹣5x+6=(x﹣2)(x﹣3) D. 6x2+2x=2x(3x+1)
查看答案长方形的面积为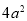 ﹣6ab+2a,若它的一边长为2a,则它的周长为( ).
﹣6ab+2a,若它的一边长为2a,则它的周长为( ).
A.4a﹣3b B.8a﹣6b C.4a﹣3b+1 D.8a﹣6b+2
查看答案如果x2+( )x+25是完全平方式,横线处填( )
A. 5 B. 10 C. ±5 D. ±10
查看答案如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
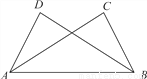
A. AC=BD B. ∠CAB=∠DBA
C. ∠C=∠D D. BC=AD
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
单项式﹣2xy5的系数是m,次数是n,则m﹣n=_____.
-8. 【解析】根据单项式的概念,可知系数为m=-2,次数为n=6,因此可得m-n=-2-6=-8. 故答案为:-8.一列单项式﹣x2,3x3,﹣5x4,7x5.…,按此规律排列,则第9个单项式是_____.
查看答案在3,﹣4,6,﹣7这四个数中,任取两个数相乘,所得的积最大的是_____.
查看答案若a、b互为倒数,则(﹣ab)2017=_____.
查看答案x2+ax﹣y﹣(bx2﹣x+9y+3)的值与x的取值无关,则﹣a+b的值为( )
A. 0 B. ﹣1 C. ﹣2 D. 2
查看答案一个多项式与x2﹣3x+2的和是3x﹣1,则这个多项式为( )
A. ﹣x2+6x+1 B. ﹣x2+1 C. ﹣x2+6x﹣3 D. ﹣x2﹣6x+1
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
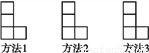
在由小正方形组成的L形的图形中,用三种不同的方法添画一个小正方形,使它成为轴对称图形.
如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律摆.
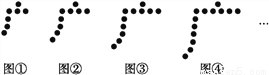
(1)第5个“广”字中的棋子个数是 .
(2)第n个“广”字需要多少枚棋子?
查看答案如图,点D在AB上,点E在AC上,AB=AC,AD=AE.试说明∠B=∠C.
先化简再求值:(a-2)2-(a-1)·(a+1)+5a,其中a=-2.
查看答案小聪和小明沿同一条路同时从学校出发到某图书馆查阅资料,学校与图书馆的路程是4 km,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线O—A—B—C和线段OD分别表示两人离学校的路程s(km)与所经过的时间t(min)之间的关系,请根据图象回答:下列四个结论
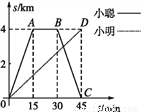
①小聪在图书馆查阅资料的时间为15 min;
②小聪返回学校的速度为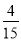 km/min;
km/min;
③小明离开学校的路程s(km)与所经过的时间t(min)之间的关系式是s=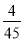 t;
t;
④当小聪与小明迎面相遇时,他们离学校的路程是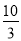 km.
km.
其中正确结论的序号是_____.
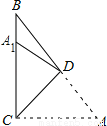
查看答案如图,△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边BC上A1处,折痕为CD,则∠A1DB=__度.
- 题型:解答题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
一个不透明的袋子,装了除颜色不同,其他没有任何区别的红色球3个,绿色球4个,黑色球7个,黄色球2个,从袋子中随机摸出一个球,摸到黑色球的概率是 .
. 【解析】 试题分析:已知红色球3个,绿色球4个,黑色球7个,黄色球2个,可得球的总数=3+4+7+2=16个,所以摸到黑色球的概率.(2015扬州)色盲是伴X染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取体检表,统计结果如表:
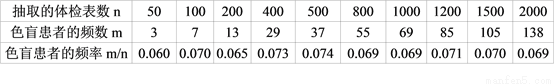
根据表中数据,估计在男性中,男性患色盲的概率为____________(结果精确到0.01)
查看答案[6a2b2+___+____]÷2ab2=3a+b-1.
查看答案在一个不透明的盒子里装有5个黑球,3个红球和2个白球,它们除颜色外其余都相同,从中随机摸出一个球,摸到红球的概率是 .
查看答案有一种原子的直径约为0.000 000 53 m,它可以用科学记数法表示为________.
查看答案如图,已知C是线段AB上的任意一点(端点除外),分别以AC,BC为边并且在AB的同一侧作等边三角形ACD和等边三角形BCE,连接AE交CD于点M,连接BD交CE于点N.给出以下三个结论:
①AE=BD;②CN=CM;③MN∥AB.其中正确结论的个数是( )

A. 0 B. 1 C. 2 D. 3
查看答案 试题属性- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
在一些美术字中,有的汉字是轴对称图形,下列四个汉字中,可以看作轴对称图形的是( )
A. B.
B. C.
C. D.
D.
下列四个图形:其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
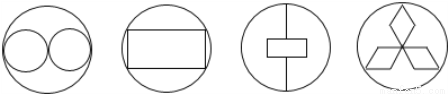
A. 1 B. 2 C. 3 D. 4
查看答案下列说法正确的是( )
A. “任意画出一个等边三角形,它是轴对称图形”是随机事件
B. 某种彩票的中奖率为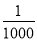 ,说明每买1 000张彩票,一定有一张中奖
,说明每买1 000张彩票,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为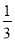
D. “概率为1的事件”是必然事件
查看答案如图所示,AB∥CD,BC平分∠ABD,若∠C=40°,则∠D的度数为 ( )
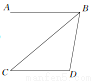
A. 90° B. 100° C. 110° D. 120°
查看答案下列计算正确的是( )
A. 4x3•2x2=8x6 B. a4+a3=a7 C. (﹣x2)5=﹣x10 D. (a﹣b)2=a2﹣b2
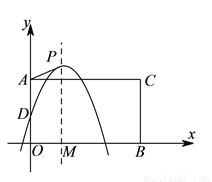
查看答案如图,在平面直角坐标系中,点 ,
,  分别是
分别是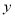 轴正半轴,
轴正半轴, 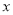 轴正半轴上两动点,
轴正半轴上两动点, 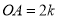 ,
, 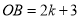 ,以
,以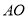 ,
, 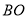 为邻边构造矩形
为邻边构造矩形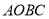 ,抛物线
,抛物线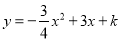 交
交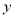 轴于点
轴于点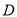 ,
, 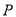 为顶点,
为顶点, 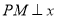 轴于点
轴于点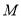 .
.
(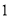 )求
)求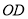 ,
, 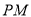 的长(结果均用含
的长(结果均用含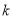 的代数式表示);
的代数式表示);
(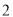 )当
)当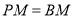 时,求该抛物线的表达式;
时,求该抛物线的表达式;
(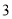 )在点
)在点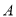 在整个运动过程中,若存在
在整个运动过程中,若存在 是等腰三角形,请求出所有满足条件的
是等腰三角形,请求出所有满足条件的 的值.
的值.
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图, 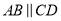 ,
, 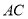 ,
, 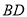 交于
交于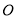 ,
, 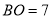 ,
, 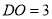 ,
, 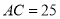 ,则
,则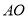 长为( ).
长为( ).
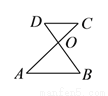
A. 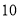 B.
B. 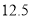 C.
C. 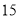 D.
D. 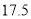
将抛物线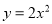 先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
A. 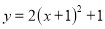 B.
B. 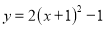 C.
C. 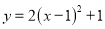 D.
D. 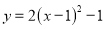
若二次函数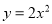 的图象经过点
的图象经过点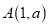 ,则
,则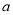 的值为( ).
的值为( ).
A. 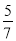 B.
B. 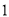 C.
C. 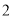 D.
D. 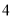
若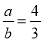 ,则
,则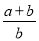 的值等于( ).
的值等于( ).
A. 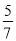 B.
B. 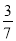 C.
C. 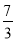 D.
D. 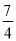
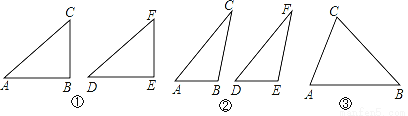
【问题提出】
学习了三角形全等的判定方法(即“SSS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,请你证明:△ABC≌△DEF(提示:过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H).
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你利用图③,在图③中用尺规作出△DEF,使△DEF和△ABC不全等.
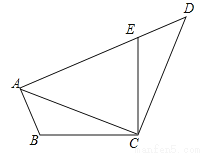
如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

