��Ŀ����
��|x|=4��|y|=7����x+y��0����ôx��y��ֵ�ǣ�������
A. 3��11 B. 3��11 C. ��3��11 D. ��3��11
D �����������ݾ���ֵ�����ʣ���֪x=��4��y����7��Ȼ�����x+y��0����֪x=4��y=7��x=-4��y=7�����x-y=4-7=-3��x-y=-4-7=-11. ��ѡ��D.������һ��A��һֻ���ϴ�A��������4����λ���ȵ���ԭ�㣬���A����ʾ�����ǣ�������
A. 4 B. ��4 C. ��8 D. ��4
�鿴��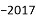
A. 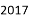
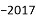
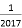 D.
D. 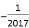
��֪����ʽA��B������A��B��ijͬѧ������ʱ��A��B������A+B���������ΪA+B=3m2��2m��5����B=2m2��3m��2����������������ȷ�𰸣�
�鿴����֪|a��2|+��b+1��2=0����5ab2��|2a2b����4ab2��2a2b��|��ֵ��
�鿴�����˾������ij������Ӫ��ȫ���ڶ��������ʤ��·�Ͻ��У�����涨��Ϊ��������Ϊ���������������г���̣���λ������ �����£�
+8��+4����10����8��+6����2����5����7��+4��+6����8����9
��1�����ڼ����˿��͵�Ŀ�ĵ�ʱ�������պûص���������㣿
��2�������һ���˿��� ��Ŀ�ĵ�ʱ������������������Զ��
��3��������������Ϊ0.4��/������������������Ͷ�������
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ�����
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
����60��ij�ֲ�Ʒ��������3����Ʒ����ô���������ȡ1����Ʒǡ�ó鵽��Ʒ�ĸ�����_____��
������������60����Ʒ�У�ÿһ�����鵽�Ļ����Ǿ��ȵģ� �������ȡ1��ǡ���Ǵ�Ʒ�ĸ���Ϊ��P���鵽��Ʒ��=.��ͼ��ˮƽ��������һ���Ϊ30��cm2�Ļ�ɫ����OAB������OA=6cm����OA��ֱ�ڵ��棬������������ҹ���������������B�պýӴ�����Ϊֹ������������������У���O�ƶ��ľ����ǣ�������
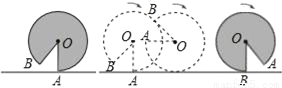
A. 10��cm B. 20��cm C. 24��cm D. 30��cm
�鿴��������x��һԪ���η���kx2��2x��1=0����������ȵ�ʵ��������k��ȡֵ��Χ�ǣ�������
A. k����1 B. k����1��k��0 C. k��1 D. k��1��k��0
�鿴����a2��4a��4�Ŀո���У��������ϡ�+�������������еõ��Ĵ���ʽ�У��ܹ�����ȫƽ��ʽ�ĸ����ǣ� ��
A. 1 B. 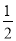 C.
C. 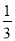 D.
D. 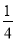
��֪�������εı߳�Ϊ2������������Բ�İ뾶Ϊ��������
A. 1 B. 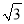 C. 2 D. 2
C. 2 D. 2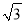
��֪һ�����ݣ�16��15��16��14��17��16��15���������ǣ�������
A. 17 B. 16 C. 15 D. 14
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��֪10m=2��10n=3����103m+2n=��������
A. 17 B. 72 C. 12 D. 36
B ����������������� ��ѡB.�ڱ߳�Ϊa������������ȥһ���߳�Ϊb��С�����Σ�a��b������������������ͼ��1����Ȼ��ƴ��һ�����Σ���ͼ��2��������������ͼ�ε������ϵ����������ʽ�ӳ������ǣ�������
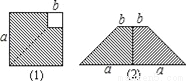
A. a2��b2=��a+b����a��b�� B. ��a+b��2=a2+2ab+b2
C. ��a��b��2=a2��2ab+b2 D. a2��b2=��a��b��2
�鿴��������ʽ�ֽⲻ��ȷ���ǣ�������
A. x2��6x+9=��x��3��2 B. x2��y2=��x��y��2
C. x2��5x+6=��x��2����x��3�� D. 6x2+2x=2x��3x+1��
�鿴�������ε����Ϊ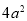 ��6ab+2a��������һ�߳�Ϊ2a���������ܳ�Ϊ�� ��.
��6ab+2a��������һ�߳�Ϊ2a���������ܳ�Ϊ�� ��.
A��4a��3b B��8a��6b C��4a��3b+1 D��8a��6b+2
�鿴�����x2+�� ��x+25����ȫƽ��ʽ�����ߴ��������
A. 5 B. 10 C. ��5 D. ��10
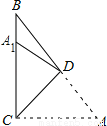
�鿴����ͼ����֪��ABC����BAD���������������������ж���ABC�ա�BAD����( )
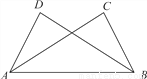
A. AC��BD B. ��CAB����DBA
C. ��C����D D. BC��AD
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
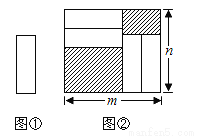
��������״��С��ȫ��ͬ��С�����ο�Ƭ����ͼ1�����ظ��ط���һ������Ϊ�����Σ���Ϊm cm����Ϊn cm���ĺ��ӵײ�����ͼ2�������ӵ���δ����Ƭ���ǵIJ�������Ӱ��ʾ����ͼ2��������Ӱ�����ܳ�����_____cm������m��n��ʽ�ӱ�ʾ����
����ʽ��2xy5��ϵ����m��������n����m��n=_____��
�鿴��һ�е���ʽ��x2��3x3����5x4��7x5���������˹������У����9������ʽ��_____��
�鿴����3����4��6����7���ĸ����У���ȡ��������ˣ����õĻ�������_____��
�鿴����a��b��Ϊ��������ab��2017=_____��
�鿴��x2+ax��y����bx2��x+9y+3����ֵ��x��ȡֵ�أ���a+b��ֵΪ��������
A. 0 B. ��1 C. ��2 D. 2
�鿴�� ��������- ���ͣ������
- �Ѷȣ�����
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
����������ȷ���ǣ�������
A. ��a2b��2a2b=��3a2b B. 2a��a=2a
C. 3a2+2a2=5a4 D. 2a+b=2ab
A �����������ݺϲ�ͬ����ķ���֪��a2b��2a2b=��3a2b��2a��a=a��3a2+2a2=5a2��2a+b���ܼ��㣬��ֻ��A��ȷ. ��ѡ��A.����ʽ �ĸ���ֱ��ǣ�������
�ĸ���ֱ��ǣ�������
A.  B.
B.  C.
C.  D.
D. 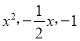
����ʽ�ӣ�x2+2�� 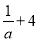 ��
�� 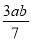 ��
�� 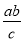 ����5x��0�У���ʽ�ĸ����У�������
����5x��0�У���ʽ�ĸ����У�������
A. 3�� B. 4�� C. 5�� D. 6��
�鿴���ҹ�����Ī�Ի��ŵ������ѧ��֮�����Ĵ�����Ʒ���ܡ����������ͱȻ�֮ǰ������180�����ﵽ2100000�ᣬ��2100000�ÿ�ѧ��������ʾΪ��������
A. 0.21��108 B. 2.1��106 C. 2.1��107 D. 21��106
�鿴���������ĺ�Ϊ��������ô���������ǣ�������
A. ���� B. ����
C. ������һ��Ϊ���� D. һ��һ��
�鿴����|x|=4��|y|=7����x+y��0����ôx��y��ֵ�ǣ�������
A. 3��11 B. 3��11 C. ��3��11 D. ��3��11
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
���˾������ij������Ӫ��ȫ���ڶ��������ʤ��·�Ͻ��У�����涨��Ϊ��������Ϊ���������������г���̣���λ������ �����£�
+8��+4����10����8��+6����2����5����7��+4��+6����8����9
��1�����ڼ����˿��͵�Ŀ�ĵ�ʱ�������պûص���������㣿
��2�������һ���˿��� ��Ŀ�ĵ�ʱ������������������Զ��
��3��������������Ϊ0.4��/������������������Ͷ�������
��1��5����2��21����3��30.8�� �������������������1������������ͼ��ɣ� ��2������������ͼ��ɣ� ��3���������·�̵ľ���ֵ�ĺͣ��ٳ���ÿ�������������. �����������1����+8+4-10-8+6=0 �ཫ�������˿��͵�Ŀ�ĵ�ʱ�������պûص����������. ��2�������һ���˿��͵�Ŀ�ĵ�ʱ�����������������ľ���Ϊ��+8+4-10-8+6-2-5-7+...�Ȼ�������ֵ��
��1��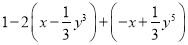 ������x=��
������x=��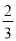 ��y=��1��
��y=��1��
��2����a2b+��3ab2��a2b����2��2ab2��a2b��������a=1��b=��2��
�鿴����������m��n�������ϵ�λ����ͼ��ʾ���뻯��|m+n|+|m��n|��|n|��
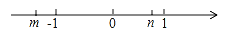
����������������A��B��C���ֱ��ʾ��3��0��2��������Ҫ��ش�
��1����A�����ƶ�6����λ���������ʾ����˭���
��2����C�����ƶ�3����λ����ʱ��B��ʾ�����ȵ�C��ʾ��������٣�
��3�������ƶ���A��B��C�е������㣬����ʹ����������ʾ������ͬ���м��ְ취���ֱ�д������
�鿴������
��1������3��+����4������+11��������9����
��2��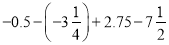 ��
��
��3��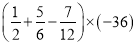 ��
��
��4��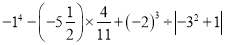 ��
��
�����и���������Ӧ�Ĵ������ڣ�
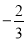 ��
�� 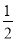 ����0.01��
����0.01�� 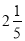 ��7��1��������4����+����1��
��7��1��������4����+����1��
��������{�� ����}
��������{�� ����}
�Ǹ���������{�� ����}
��������{�� ����}��
�鿴�� ��������- ���ͣ������
- �Ѷȣ�����
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
����ʽ��2xy5��ϵ����m��������n����m��n=_____��
��8�� �����������ݵ���ʽ�ĸ����֪ϵ��Ϊm=-2������Ϊn=6����˿ɵ�m-n=-2-6=-8. �ʴ�Ϊ��-8.һ�е���ʽ��x2��3x3����5x4��7x5���������˹������У����9������ʽ��_____��
�鿴����3����4��6����7���ĸ����У���ȡ��������ˣ����õĻ�������_____��
�鿴����a��b��Ϊ��������ab��2017=_____��
�鿴��x2+ax��y����bx2��x+9y+3����ֵ��x��ȡֵ�أ���a+b��ֵΪ��������
A. 0 B. ��1 C. ��2 D. 2
�鿴��һ������ʽ��x2��3x+2�ĺ���3x��1�����������ʽΪ��������
A. ��x2+6x+1 B. ��x2+1 C. ��x2+6x��3 D. ��x2��6x+1
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
����С��������ɵ�L�ε�ͼ����,�����ֲ�ͬ�ķ�������һ��С������,ʹ����Ϊ��Գ�ͼ��.
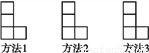
��ͼ��,ͼ��,ͼ��,ͼ��,��,����Χ�����Ӱ���ij�ֹ��ɰڳɵ�һ�С��㡱��,�������ֹ��ɰ�.
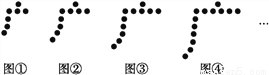
(1)��5�����㡱���е����Ӹ���������������.
(2)��n�����㡱����Ҫ����ö����?
�鿴����ͼ,��D��AB��,��E��AC��,AB=AC,AD=AE.��˵����B=��C.
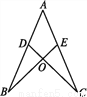
�Ȼ�������ֵ:(a-2)2-(a-1)��(a+1)+5a,����a=-2.
�鿴��С�Ϻ�С����ͬһ��·ͬʱ��ѧУ������ijͼ��ݲ�������,ѧУ��ͼ��ݵ�·����4 km,С�������г�,С������,��С�ϴ�ԭ·�ص�ѧУʱ,С���պõ���ͼ���,ͼ������O��A��B��C���߶�OD�ֱ��ʾ������ѧУ��·��s(km)����������ʱ��t(min)֮��Ĺ�ϵ,�����ͼ��ش�:�����ĸ�����
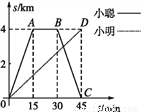
��С����ͼ��ݲ������ϵ�ʱ��Ϊ15 min;
��С�Ϸ���ѧУ���ٶ�Ϊ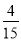 km/min;
km/min;
��С���뿪ѧУ��·��s(km)����������ʱ��t(min)֮��Ĺ�ϵʽ��s=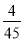 t;
t;
�ܵ�С����С��ӭ������ʱ,������ѧУ��·����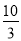 km.
km.
������ȷ���۵������_____.
�鿴����ͼ����ABC�У���ACB=90�㣬��A=50�㣬�����۵���ʹ��A���ڱ�BC��A1�����ۺ�ΪCD�����A1DB=__�ȣ�
- ���ͣ������
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ�� 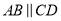 ��
�� 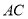 ��
�� 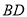 ����
����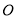 ��
�� 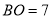 ��
�� 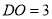 ��
�� 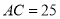 ����
���� ���� ����
���� ����
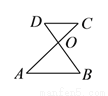
A.  B.
B.  C.
C. 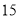 D.
D. 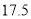
��������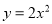 ������ƽ��һ����λ��������ƽ��һ����λ������ƽ�ƺ�õ��������߽���ʽΪ�� ����
������ƽ��һ����λ��������ƽ��һ����λ������ƽ�ƺ�õ��������߽���ʽΪ�� ����
A. 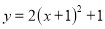 B.
B. 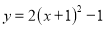 C.
C. 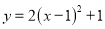 D.
D. 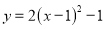
�����κ���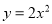 ��ͼ����
��ͼ����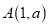 ����
����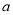 ��ֵΪ�� ����
��ֵΪ�� ����
A. 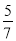 B.
B. 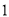 C.
C. 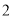 D.
D. 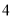
��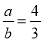 ����
����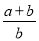 ��ֵ���ڣ� ����
��ֵ���ڣ� ����
A. 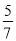 B.
B. 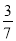 C.
C. 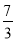 D.
D. 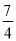
�����������
ѧϰ��������ȫ�ȵ��ж�����������SSS������ASA������AAS������SSS������ֱ��������ȫ�ȵ��ж�����������HL���������Ǽ����ԡ������������������ߺ�����һ�ߵĶԽǶ�Ӧ��ȡ������ν����о���
������˼����
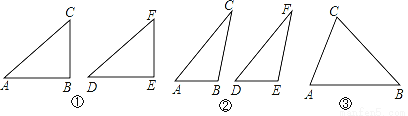
���Dz����������÷������Ա�ʾΪ���ڡ�ABC�͡�DEF�У�AC=DF��BC=EF����B=��E��Ȼ�ԡ�B���з��࣬�ɷ�Ϊ����B��ֱ�ǡ��۽ǡ���ǡ������������̽����
������̽����
��һ�����������B��ֱ��ʱ����ABC�ա�DEF��
��ͼ�٣��ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E=90�㣬������ ��������֪��Rt��ABC��Rt��DEF��
�ڶ������������B�Ƕ۽�ʱ����ABC�ա�DEF��
��ͼ�ڣ��ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E���ҡ�B����E���Ƕ۽ǣ�����֤������ABC�ա�DEF����ʾ������C��CG��AB��AB���ӳ�����G������F��FH��DE��DE���ӳ�����H����
���������������B�����ʱ����ABC�͡�DEF��һ��ȫ�ȣ�
�ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E���ҡ�B����E������ǣ���������ͼ�ۣ���ͼ�����ó߹�������DEF��ʹ��DEF�͡�ABC��ȫ�ȣ�
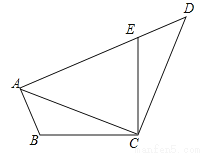
��ͼ����֪���ı���ABCD�У���E��AD�ϣ���BCE=��ACD=90�㣬��BAC=��D��BC=CE��
��1����֤��AC=CD��
��2����AC=AE�����DEC�Ķ�����
- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������