Question

2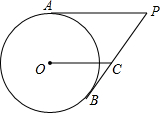．如图，PA，PB分别与⊙O相切于点A，B，OC∥AP交PB于C．
（1）求证：AP=OC+BC；
（2）若⊙O的半径为4，PA=8，求BC的长．

Answer 1

分析 （1）连接OP．由PA、PB是切线，推出∠1=∠2，PA=PB，由OC∥PA，PA=PB，推出∠1=∠3，推出∠2=∠3，推出OC=PC，由此即可证明．
（2）利用（1）的结论即可解决问题．

解答 （1）证明：如图，连接OP．

∵PA、PB是切线，
∴∠1=∠2，
∵OC∥PA，PA=PB，
∴∠1=∠3，
∴∠2=∠3，
∴OC=PC，
∴AP=PB=BC+PC=BC+OC．

（2）由（1）可知，PA=OC+BC，
∵PA=8，OC=4，
∴BC=8-4=4．

点评 本题考查切线的性质、切线长定理、平行线的判定和性质等知识，解题的关键是熟练掌握这些知识，学会添加常用辅助线，属于中考常考题型．